倒立摆系统的建模、分析与设计

倒立摆系统的建模、分析与设计

引用

CSDN

1.

https://blog.csdn.net/m0_58209778/article/details/139448174

倒立摆系统是一种典型的非线性控制对象，广泛应用于控制理论的教学和研究中。本文将介绍倒立摆系统的建模、分析与设计过程，包括系统稳定性分析、状态反馈控制器设计以及降维状态观测器的实现。

一、案例背景

倒立摆系统是一个经典的控制理论研究对象，其主要特点是具有非线性、不稳定性和多输入多输出特性。通过建立倒立摆系统的线性状态空间模型，可以对其进行深入的分析和设计。

二、建模分析

由PDF知，倒立摆系统的线性状态空间表达式为：

则有：

2.1 系统稳定性、能控性和能观性分析

在Matlab环境下，可以分析系统的稳定性、能控性和能观性。以下是具体的代码实现：

%{
1.在Matlab 环境下，分析系统的稳定性、能控性及能观性。
%}
A = [0 1 0 0;20.601 0 0 0; 0 0 0 1;-0.4905 0 0 0];
B = [0;-1;0;0.5];
C = [1 0 0 0;0 0 1 0];
n = size(A, 1)
% 系统的状态空间表示
sys = ss(A, B, C, 0);
% 稳定性分析
%计算特征值
eigenvalues = eig(A)
if all(real(eigenvalues) < 0)
    disp('系统是稳定的.');
else
    disp('系统是不稳定的.');
end
% 能控性分析
Uc = [B, A*B, A^2*B,A^3*B];
rank_Uc = rank(Uc)
if rank_Uc == n
    disp('系统是能控的.');
else
    disp('系统是不能控的.');
end
% 能观性分析
Uo = [C; C*A; C*A^2;C*A^3];
rank_Uo = rank(Uo)
if rank_Uo == n
    disp('系统是能观的.');
else
    disp('系统是不能观的.');
end

结果显示，该系统不稳定，但是能控能观。

2.2 开环仿真验证

在SIMULINK环境下，可以进行系统开环仿真，验证系统的稳定性。具体步骤如下：

1. 连接State-Space块的输出到Scope块的输入。
2. 连接Step块的输出到State-Space块的输入。
3. 配置State-Space块的系统状态空间矩阵（A、B、C、D）。
4. 设置Step块的阶跃信号参数。
5. 调整Scope块的显示参数。
6. 运行仿真并查看系统的响应。

通过这些步骤，可以在SIMULINK中建立一个简单的系统，并使用State-Space块描述系统的动态行为，Step块产生一个阶跃信号作为输入，Scope块用于查看系统的输出响应。结果显示，系统是不稳定的。

三、状态反馈控制器设计

由倒立摆系统的线性状态空间表达式可得系统的状态方程和输出方程。以下是状态反馈控制器的设计过程：

3.1 计算反馈增益阵

%{
![](https://wy-static.wenxiaobai.com/chat-rag-image/543902043865540000)
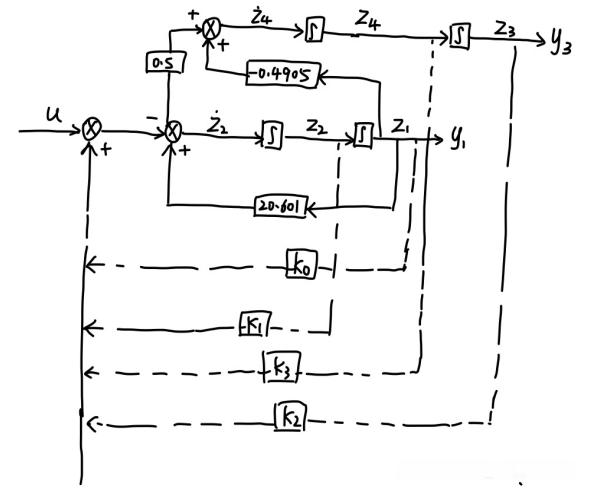
在SIMULINK环境下，给定系统期望的极点，设计状态反馈控制器，
并通过仿真验证其性能
%}
% 定义系统矩阵
A = [0 1 0 0; 20.601 0 0 0; 0 0 0 1; -0.4905 0 0 0];
B = [0; -1; 0; 0.5];
C = [1 0 0 0; 0 0 1 0];
D = [0; 0];
% 计算可控性矩阵
Co = ctrb(A, B);
% 检查可控性
rank_Co = rank(Co);
if rank_Co == size(A, 1)
    disp('系统是可控的。');
else
    error('系统不可控，请重新设计系统或控制器。');
end
% 给定的期望闭环极点
desired_poles = [-2, -3, -4, -5];
% 计算状态反馈增益矩阵 K
K = place(A, B, desired_poles)

3.2 建立Simulink模型

建立Simulink模型并运行仿真，观察四个状态的变化。实验结果表明，倒立摆很短时间内收敛到0，控制效果很好。

四、降维状态观测器设计

4.1 设计降维状态观测器

将观测值代入状态反馈建立Simulink模型（降维状态观测器）。为了简化框图，将原系统模型替换成了直接State space表示的形式，具体设置为：这里给定倒立摆角度的初值1，其他全部设为0。

4.2 仿真验证

运行仿真，观察四个状态的变化。将未加入观测器时的状态与加入状态观测器的状态作差，发现比较观测器观测值与实际状态的误差的时候，发现观测器已经能够很好地跟踪未知状态了。

通过以上分析和设计过程，可以发现倒立摆系统虽然不稳定，但通过合理的控制器设计和状态观测器的实现，可以达到良好的控制效果。