模型优化：XGBoost学习曲线及改进，泛化误差

模型优化：XGBoost学习曲线及改进，泛化误差

引用

CSDN

1.

https://blog.csdn.net/shyjhyp11/article/details/136362080

本文将探讨如何通过学习曲线和泛化误差来优化XGBoost模型的n_estimators参数。通过分析模型在不同参数设置下的表现，我们可以更好地理解模型的过拟合和欠拟合问题，并找到最优的参数配置。

基本模型实现

首先，我们加载数据并划分训练集和测试集：

from xgboost import XGBRegressor as XGBR
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.linear_model import LinearRegression as LR
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split, cross_val_score as CV, KFold
from sklearn.metrics import mean_squared_error as MSE
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from time import time
import datetime

# 加载数据
data = load_boston()
X = data.data
y = data.target

# 划分数据集
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.3, random_state=420)

# 定位模型，进行fit
reg = XGBR(n_estimators=100).fit(Xtrain, ytrain)

# 进行预测
reg.predict(Xtest)
reg.score(Xtest, ytest)  # 返回的是R平方
MSE(ytest, reg.predict(Xtest))
reg.feature_importances_

# 查看SKLEARN中所有的模型评估指标
import sklearn
sorted(sklearn.metrics.SCORERS.keys())

交叉验证

使用交叉验证来评估模型性能：

# 交叉验证，与线性回归随机森林进行结果比对
reg = XGBR(n_estimators=100)
from sklearn.model_selection import train_test_split, cross_val_score
cross_val_score(reg, Xtrain, ytrain, cv=5).mean()

# 交叉验证既可以解决数据集的数据量不够大问题，也可以解决参数调优的问题。
# 这块主要有三种方式：简单交叉验证（HoldOut检验）、k折交叉验证（k-fold交叉验证）
cross_val_score(reg, Xtrain, ytrain, cv=5, scoring="neg_mean_squared_error").mean()

绘制学习曲线

定义绘制学习曲线的函数：

def plot_learning_curve(estimator, title, X, y,
                       ax=None,  # 选择子图
                       ylim=None,  # 设置纵坐标的取值范围
                       cv=None,  # 交叉验证
                       n_jobs=None):
    from sklearn.model_selection import learning_curve
    train_sizes, train_scores, test_scores = learning_curve(estimator, X, y, shuffle=True,
                                                           cv=cv, random_state=420, n_jobs=n_jobs)
    if ax == None:
        ax = plt.gca()
    else:
        ax = plt.figure()
    ax.set_title(title)
    if ylim is not None:
        ax.set_ylim(*ylim)
    ax.set_xlabel("Traing example")
    ax.set_ylabel("Score")
    ax.grid()  # 绘制网格
    ax.plot(train_sizes, np.mean(train_scores, axis=1), "o-", color="r", label="traing score")
    ax.plot(train_sizes, np.mean(test_scores, axis=1), "o-", color="g", label="test.py score")
    ax.legend(loc="best")
    return ax

# 学习曲线的绘制
cv = KFold(n_splits=5, shuffle=True, random_state=42)
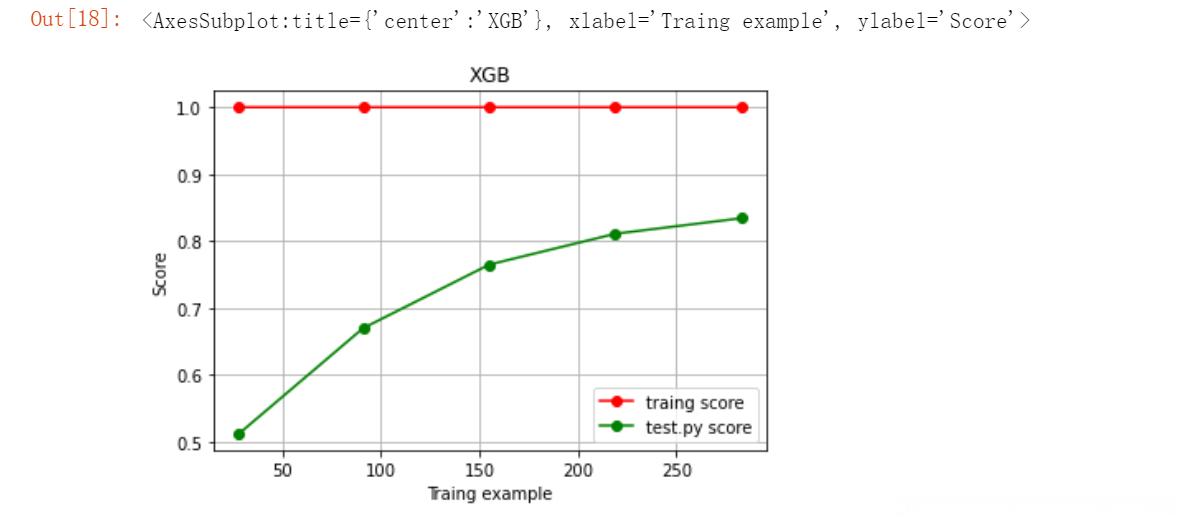
plot_learning_curve(XGBR(n_estimators=100, random_state=420), "XGB", Xtrain, ytrain, ax=None, cv=cv)

分析n_estimators参数的影响

通过绘制学习曲线来观察n_estimators参数对模型的影响：

# 绘制学习曲线，查看n_estimators对模型的影响
axis = range(10, 50, 1)
rs = []
for i in axis:
    reg = XGBR(n_estimators=i)
    cv1 = cross_val_score(reg, Xtrain, ytrain, cv=5).mean()
    rs.append(cv1)
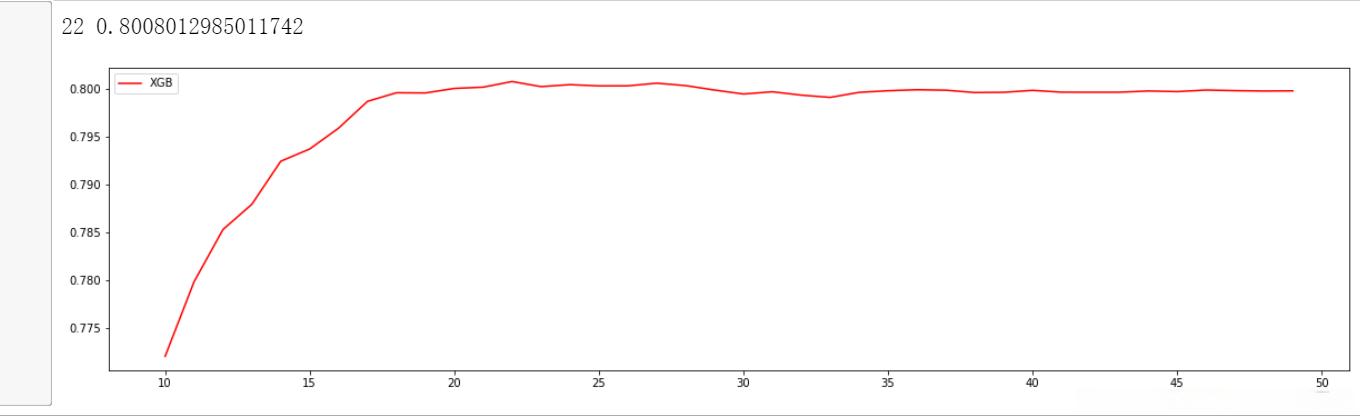
print(axis[rs.index(max(rs))], max(rs))
plt.figure(figsize=(20, 5))
![](https://wy-static.wenxiaobai.com/chat-rag-image/1454955827738725364)
plt.plot(axis, rs, c='red', label="XGB")
plt.legend()
plt.show()

泛化误差分析

泛化误差是用来衡量模型在未知数据集上的准确率：

# 绘制学习曲线，查看n_estimators对模型的影响
axis = range(10, 50, 1)
rs = []  # 偏差，衡量的是准确率
var = []  # 方差，衡量的是稳定性
ge = []  # 泛化误差的可控部门
for i in axis:
    reg = XGBR(n_estimators=i)
    cv1 = cross_val_score(reg, Xtrain, ytrain, cv=5)
    rs.append(cv1.mean())  # 记录偏差，返回的R平方就是偏差部门，衡量的是准确率
![](https://wy-static.wenxiaobai.com/chat-rag-image/6856216781637300900)
    var.append(cv1.var())
    ge.append((1 - cv1.mean()) ** 2 + cv1.var())
print(axis[rs.index(max(rs))], max(rs), var[rs.index(max(rs))])
print(axis[var.index(min(var))], rs[var.index(min(var))], min(var))
print(axis[ge.index(min(ge))], rs[ge.index(min(ge))], var[ge.index(min(ge))], min(ge))
plt.figure(figsize=(20, 5))
plt.plot(axis, rs, c='red', label="XGB")
plt.legend()
plt.show()

进一步分析

通过绘制学习曲线来观察n_estimators参数对模型的影响：

# 绘制学习曲线，查看n_estimators对模型的影响
axis = range(10, 30, 1)
rs = []  # 偏差，衡量的是准确率
var = []  # 方差，衡量的是稳定性
ge = []  # 泛化误差的可控部门
for i in axis:
    reg = XGBR(n_estimators=i)
    cv1 = cross_val_score(reg, Xtrain, ytrain, cv=5)
    rs.append(cv1.mean())  # 记录偏差，返回的R平方就是偏差部门，衡量的是准确率
    var.append(cv1.var())
    ge.append((1 - cv1.mean()) ** 2 + cv1.var())
print(axis[rs.index(max(rs))], max(rs), var[rs.index(max(rs))])
print(axis[var.index(min(var))], rs[var.index(min(var))], min(var))
print(axis[ge.index(min(ge))], rs[ge.index(min(ge))], var[ge.index(min(ge))], min(ge))
# 添加方差线条
rs = np.array(rs)
var = np.array(var)  # 源代码这里*0.01
plt.figure(figsize=(20, 5))
plt.plot(axis, rs, c='red', label="XGB")
plt.plot(axis, rs + var, c="black", linestyle="-.")
plt.plot(axis, rs - var, c="black", linestyle="-.")
plt.legend()
plt.show()

泛化误差的可控部分

plt.figure(figsize=(20, 5))
plt.plot(axis, ge, c='red', label="XGB")
plt.legend()
plt.show()

结论

从这个过程中观察n_estimators参数对模型的影响，我们可以得出以下结论：

1. XGB中的树的数量决定了模型的学习能力，树的数量越多，模型的学习能力越强。只要XGB中树的数量足够了，即便只有很少的数据，模型也能够学到训练数据100%的信息，所以XGB也是天生过拟合的模型。但在这种情况下，模型会变得非常不稳定。

2. XGB中树的数量很少的时候，对模型的影响较大，当树的数量已经很多的时候，对模型的影响比较小，只能有微弱的变化。当数据本身就处于过拟合的时候，再使用过多的树能达到的效果甚微，反而浪费计算资源。当唯一指标或者准确率给出的n_estimators看起来不太可靠的时候，我们可以改造学习曲线来帮助我们。

3. 树的数量提升对模型的影响有极限，最开始，模型的表现会随着XGB的树的数量一起提升，但到达某个点之后，树的数量越多，模型的效果会逐步下降，这也说明了暴力增加n_estimators不一定有效果。

这些都和随机森林中的参数n_estimators表现出一致的状态。在随机森林中我们总是先调整n_estimators，当n_estimators的极限已达到，我们才考虑其他参数，但XGB中的状况明显更加复杂，当数据集不太寻常的时候会更加复杂。这是我们要给出的第一个超参数，因此还是建议优先调整n_estimators，一般都不会建议一个太大的数目，300以下为佳。

本文原文来自CSDN