时间序列平滑和异常检测利器：tsmoothie库详解

创作时间:

作者:

@小白创作中心

时间序列平滑和异常检测利器：tsmoothie库详解

引用

来源

https://wangzhefeng.com/note/2024/04/12/timeseries-lib-tsmoothie/

时间序列分析是数据分析领域的重要分支，广泛应用于金融、气象、生物医学等多个领域。在时间序列分析中，数据平滑和异常检测是两个核心问题。数据平滑可以帮助去除噪声，揭示数据的内在趋势；异常检测则有助于识别数据中的异常点，为后续分析提供更准确的数据基础。本文将介绍一个功能强大的Python库——tsmoothie，它提供了多种平滑技术和异常检测方法，能够帮助用户高效地处理时间序列数据。

tsmoothie：时间序列平滑和异常检测

tsmoothie是一个Python库，用于向量化方式的时间序列平滑和异常值检测。

去噪
异常值剔除
保留原始数据中存在的时间模式

tsmoothie 平滑技术

tsmoothie使用了多种平滑技术：

指数平滑（Exponential Smoothing）
卷积平滑（Convolutional Smoothing）
constant
hanning
hamming
bartlett
blackman
傅里叶变换频谱平滑（Spectral Smoothing with Fourier Transform）
多项式平滑（Polynomial Smoothing）
样条平滑（Spline Smoothing）
linear
cubic
natural
高斯平滑（Gaussian Smoothing）
分箱平滑（Binner Smoothing）
局部加权回归散点平滑法（LOWESS）
季节性分解平滑（Seasonal Decompose Smoothing）
卡尔曼平滑（Kalman Smoothing），支持自定义组件
level
trend
seasonality
long seasonality

LOWESS

局部加权回归散点平滑法（LOWESS）是一种查看二维变量之间关系的有力工具。其主要思想是取一定比例的局部数据，在这部分子集中拟合多项式回归曲线。将局部范围从左往右依次推进，最终一条连续的曲线就被计算出来了。曲线的平滑程度与选取数据比例有关：比例越少，拟合越不平滑（因为过于看重局部性质），反之越平滑。

区间计算

tsmoothie提供了作为平滑过程结果的区间计算，这对于识别时间序列中的异常值非常有用。区间类型包括：

sigma interval
confidence interval
predictions interval
kalman interval

tsmoothie可以进行滑动平滑的方法来模拟在线使用。这可以将时间序列分成大小相等的部分并独立平滑它们。与往常一样，此功能通过WindowWrapper类以矢量化方式实现。

Bootstrap 算法

tsmoothie可以通过BootstrappingWrapper类操作时序引导，用到的Bootstrap算法有：

none overlapping block bootstrap
moving block bootstrap
circular block bootstrap
stationary bootstrap

tsmoothie 安装

$ pip install tsmoothie

tsmoothie 使用

tsmoothie 平滑 demo

随机游走数据平滑

import numpy as np
import matplotlib.pyplot as plt
from tsmoothie.utils_func import sim_randomwalk
from tsmoothie.smoother import LowessSmoother

# 生成3个长度为200的随机游走数据
np.random.seed(123)
data = sim_randomwalk(
    n_series = 3,
    timesteps = 200,
    process_noise = 10,
    measure_noise = 30,
)

# 平滑处理
smoother = LowessSmoother(smooth_fraction = 0.1, iterations = 1)
smoother.smooth(data)

# 生成区间
low, up = smoother.get_intervals("prediction_interval")

# 绘制平滑后的时序数据及其区间
plt.figure(figsize = (18, 5))
for i in range(3):
    plt.subplot(1, 3, i + 1)
    plt.plot(smoother.smooth_data[i], linewidth = 3, color = "blue")
    plt.plot(smoother.data[i], ".k")
    plt.title(f"timeseries {i + 1}")
    plt.xlabel("time")
    plt.fill_between(
        range(len(smoother.data[i])),
        low[i],
        up[i],
        alpha = 0.3,
    )

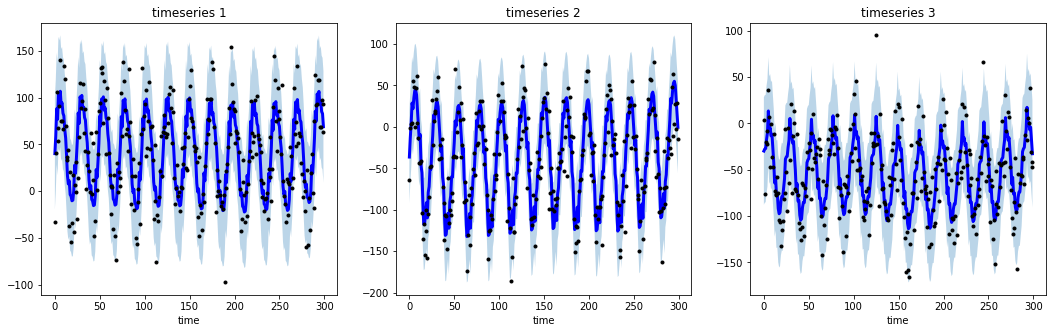
季节性数据平滑

import numpy as np
import matplotlib.pyplot as plt
from tsmoothie.utils_func import sim_seasonal_data
from tsmoothie.smoother import DecomposeSmoother

# 生成3个周期性时序数据
np.random.seed(123)
data = sim_seasonal_data(
    n_series = 3, 
    timesteps = 300, 
    freq = 24, 
    measure_noise = 30
)

# 平滑处理
smoother = DecomposeSmoother(
    smooth_type = 'lowess', 
    periods = 24,
    smooth_fraction = 0.3
)
smoother.smooth(data)

# 生成区间
low, up = smoother.get_intervals('sigma_interval')

# 绘制平滑后的时序数据及其区间
plt.figure(figsize = (18, 5))
for i in range(3):
    plt.subplot(1, 3, i + 1)
    plt.plot(smoother.smooth_data[i], linewidth = 3, color = 'blue')
    plt.plot(smoother.data[i], '.k')
    plt.title(f"timeseries {i+1}")
    plt.xlabel('time')
    plt.fill_between(
        range(len(smoother.data[i])), 
        low[i], 
        up[i], 
        alpha = 0.3
    )

tsmoothie Bootstrap demo

import numpy as np
import matplotlib.pyplot as plt
![](https://wy-static.wenxiaobai.com/chat-rag-image/3969294088609621952)
from tsmoothie.utils_func import sim_seasonal_data
from tsmoothie.smoother import ConvolutionSmoother
from tsmoothie.bootstrap import BootstrappingWrapper

# 生成周期性时序数据
np.random.seed(123)
data = sim_seasonal_data(
    n_series = 1, 
    timesteps = 300, 
    freq = 24, 
    measure_noise = 15
)

# Bootstrap处理
bts = BootstrappingWrapper(
    ConvolutionSmoother(
        window_len = 8, 
        window_type = 'ones'
    ), 
    bootstrap_type = 'mbb', 
    block_length = 24
)
bts_samples = bts.sample(data, n_samples = 100)

# 绘制Bootstrap后的时序数据
plt.figure(figsize = (13, 5))
plt.plot(bts_samples.T, alpha = 0.3, c = 'orange')
plt.plot(data[0], c = 'blue', linewidth = 2)