简单，却又反直觉的“三门问题”，暴露出很多人根本不懂“概率”

简单，却又反直觉的“三门问题”，暴露出很多人根本不懂“概率”

引用

网易

1.

https://www.163.com/dy/article/JEQII9Q60521F5QQ.html

在概率论中，有一个经典的问题被称为“三门问题”，它源自一个电视游戏节目。这个问题看似简单，却因为其反直觉的答案而困扰了很多人。本文将通过详细的解释和图示，帮助读者彻底理解这个问题。

设想你正在参加一个活动。
在你面前有三扇门，其中一扇门后有一辆豪车，另外两扇门后是空的。
你可以选择其中一扇门，如果选中了豪车，豪车就归你了。

在你选择一扇门后，活动的主持人并不会直接打开那扇门，而是会打开另外两扇门的某一扇门，结果是空门。
请问你要不要换门，选择另外两扇门中还没被打开的门？

上面的场景就是“三门问题”，需要注意的是：主持人并不是碰巧打开了一扇空门，而是知道门后的场景，故意打开了一扇空门。
此时，为了提高中奖率，换门是明智的选择，而且会直接让中奖率翻倍。

原本在三扇门中选一扇门，中奖率只有三分之一，可以记为：1/3。

换门之后，中奖率会直接变成三分之二，可以记为：2/3。
不过很多人都认为上面的概率是错的，他们认为主持人排除了一扇空门之后，剩下的两扇门开出豪车的概率都会增加，不管换不换门，中奖率都是二分之一，可以记为：1/2。
这种想法也并不是完全错误，不过要把前提条件改成：主持人不知道门后的场景，只是碰巧打开了一扇空门。
注意，是否应该换门，完全取决于：主持人打开一扇空门，是故意的？还是不小心的？
先来看一个“自作聪明”的理解
很多人会用一种另类的方法理解“三门问题”，他们的做法是：
假设有100扇门，选中豪车的概率只有1%，豪车在没选的门内的概率是99%
现在把没选的99扇门挨个打开，已经打开98扇门了，结果全是空门。这就相当于把99扇门的99%的中奖率，全都转移给了还没打开的那扇没选的门。
到这个时候，谁还会笨到不知道换门？
只有3扇门的时候也一样，豪车在没选的门内有2/3的概率，现在都转移到了还没打开的那扇没选的门。
当然应该换门。

上面的那种解释怎么样？
我只想说四个字：自作聪明。
因为上面那种解释和“三门问题”的精髓根本就不沾边，说了一大堆，结果还不如不说。
我还是想强调，在“三门问题”中，是否应该换门，完全取决于：主持人打开一扇空门，是故意的？还是不小心的？

就算假设有100扇门，也必须先说清楚：打开98扇空门，究竟是必然事件？还是偶然事件？

如果是在没选的99扇门中，随机打开98扇门，碰巧都是空门。那么不管换不换门，选中豪车的概率都是50%，换门毫无意义。

如果是在没选的99扇门中，有计划地打开98扇门，确保都是空门。那么换门以后，选中豪车的概率就会涨到99%，换门有意义。
怎么解释？
能说清楚“故意”和“不小心”对概率的影响，才算是理解了“三门问题”。

条件概率
是故意的？还是不小心的？这两者究竟有什么区别？
这种问题，说简单也简单，“不小心开空门”的情况和条件概率有些关系（当然，“故意开空门”的情况已经不是条件概率，欢迎大家讨论）。
如果有两个事件，分别记为A和B，我们可以用：

P(A)表示A事件发生的概率

P(B)表示B事件发生的概率

P(AB)表示A事件和B事件都发生的概率

P(A|B)表示在B事件发生的条件下，A事件发生的概率
P(A|B)就是条件概率，很容易可以发现这样一个公式：
上面的公式就是条件概率公式。
回到“三门问题”，我们先考虑“主持人不小心打开空门”的情况。
定义：

A事件：一开始就选中豪车

B事件：主持人打开空门

C事件：换门之后选中豪车
计算概率之前，需要先列出样本空间，也就是可能发生的所有情况（样本）：

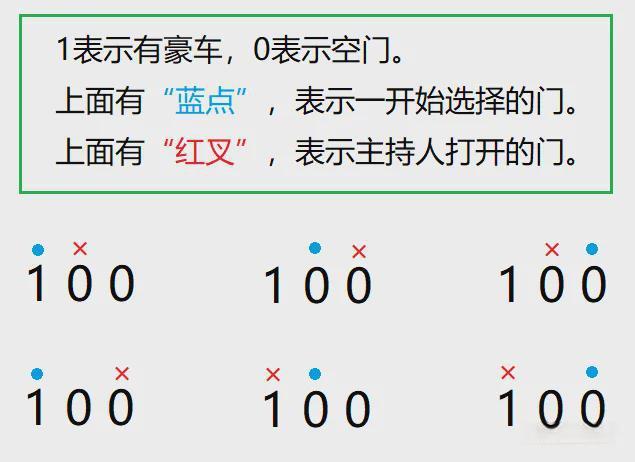
如上图所示，一共有6种情况，每一种情况发生的概率都是相同的。
根据上面的图片，可以轻松算出条件概率：
可以看出，“主持人不小心打开空门”的情况下，不管换不换门，中奖率都是1/2。

现在再考虑“主持人故意打开空门”的情况，有一种想法是，此时，B事件发生的概率等于1，所以只需要对上面的计算过程做一个小改动：
这样确实可以得到：不换门的中奖率只有1/3。
但是这种做法根本行不通，只要按相同的方法再算一个条件概率，就会发现问题。
换门的中奖率只有1/3。
总共就三扇门，主持人排除了一扇门，豪车必然在剩下的两扇门中。剩下的两扇门，各自的中奖率加起来应该是100%才对。
但是按上面的计算方法，剩下的两扇门，各自的中奖率都是1/3，加起来竟然不是100%！
到底哪里出了问题？

样本的“消除”与“转移”
一开始可以认为共有6种情况（样本），每一种情况发生的概率都相同，其中有2种是“主持人没打开空门”的情况。
“主持人不小心打开空门”，可以发生那2种情况，只是不统计那2种情况，让样本空间变成了4种概率相同的情况。
可以直接看出，不管换不换门，中奖率都是1/2。

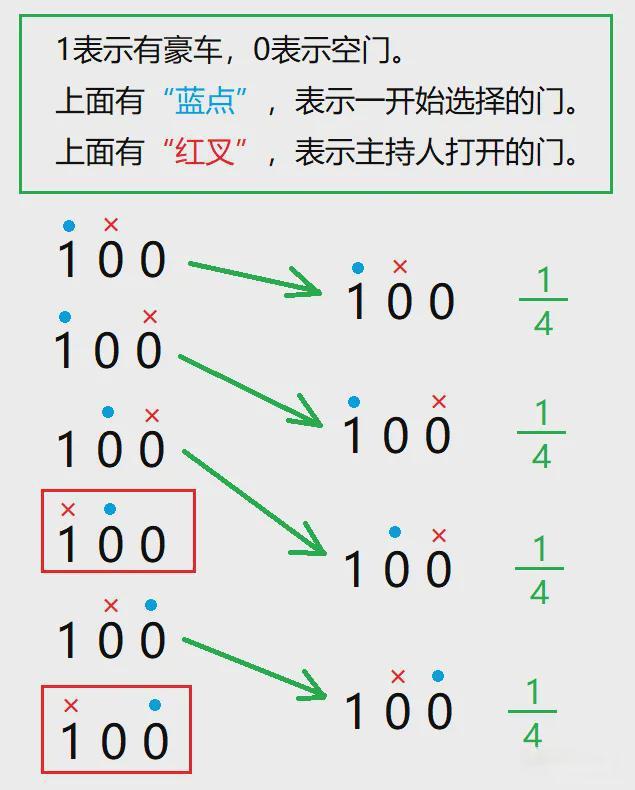
“主持人故意打开空门”，是完全不让那2种情况发生。
回到你选择了一扇门的那一步，此时的样本空间有3种情况，每一种情况发生的概率都相同，都是1/3。
如果你一开始就选中了豪车，主持人就要在剩下的两扇空门中选择一扇打开。这1种情况就“分裂”成了2种情况，“分裂”之后的2种情况的概率都是1/6。
如果你一开始选中了一扇空门，主持人就不必再做选择，直接打开你没选的空门就行了。这种情况不存在“分裂”，始终都是原本的概率：1/3。
借助下面的图片，可以直接看出，不换门的中奖率都是1/3，换门的中奖率都是2/3。

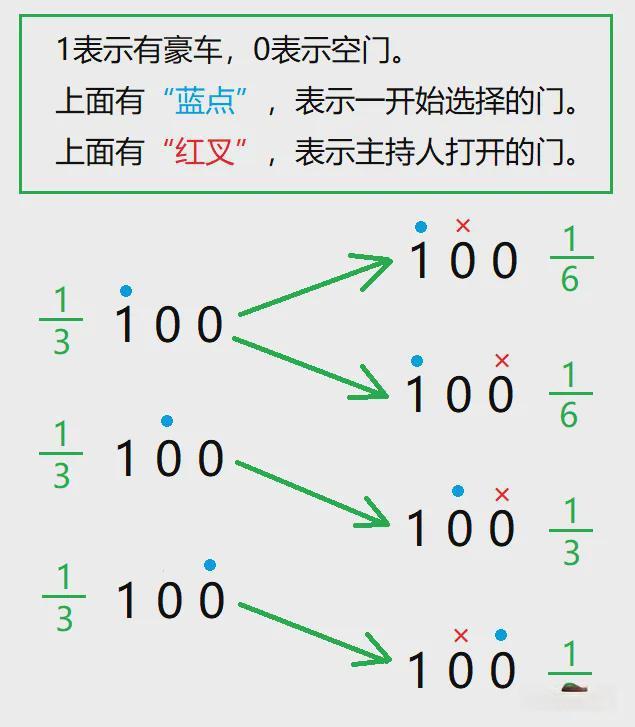
我相信上面的图片已经很直观的展现了“故意”和“不小心”的区别。

“不小心”是在“消除”一部分样本。

“故意”是在“转移”一部分样本。
现在，大家应该对“三门问题”没什么问题了吧？