数据科学中的数据分布:正态分布、二项分布和均匀分布
数据科学中的数据分布:正态分布、二项分布和均匀分布
在数据科学领域,了解数据分布是进行有效数据分析、可视化和模型构建的基础。本文将带你深入理解正态分布、二项分布和均匀分布等常见数据分布类型,并通过Python代码示例展示如何生成和可视化这些分布。
对于有效的数据分析、可视化和模型构建来说,了解数据的分布至关重要。如果数据集具有倾斜分布,则表示数据点分布不均匀,并且倾向于向右或向左倾斜。 这可能导致模型不准确地预测来自代表性不足的组的数据点,或者根据不适当的指标进行优化。
下面是了解数据分布可增强机器学习模型准确性的关键方面。
步骤 | 说明 |
|---|---|
探索性数据分析 (EDA) | 了解数据的分布可更轻松地探索新的数据集和查找模式。 |
数据预处理 | 某些预处理技术(例如规范化或标准化)用于使数据更加正态分布,这是许多模型中的常见假设。 |
模型选择 | 不同的模型对数据的分布做出不同的假设。 例如,某些模型假设数据是正态分布的,如果违反此假设,模型可能表现不佳。 |
提高模型性能 | 转换目标变量来减少偏度可使目标线性化,这对许多模型都很有用。 这可以减少误差范围,还可能提高模型的性能。 |
模型相关性 | 将模型部署到生产环境后,请务必使其在最新数据的上下文中保持相关性。 如果存在数据倾斜,即数据分布在生产中与训练期间使用的内容相比发生了变化,则模型可能会脱离上下文。 |
了解数据分布可增强模型构建过程。 通过它,你可识别特征和目标中随机变量的均值、扩散和范围来建立更准确的假设。
让我们来探讨一些最常见的数据分布类型,例如正态分布、二项分布和均匀分布。
正态分布
正态分布由均值和标准偏差这两个参数表示。 均值指示钟形曲线的中心位置,标准偏差指示分布的扩散。
让我们来看一个正态分布特征的示例。 下面的代码生成用于
var
特征的数据来进行演示。
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
# Set the mean and standard deviation
mu, sigma = 0, 0.1
# Generate a normally distributed variable
var = np.random.normal(mu, sigma, 1000)
# Create a histogram of the variable using seaborn's histplot
sns.histplot(var, bins=30, kde=True)
# Add title and labels
plt.title('Histogram of Normally Distributed Variable')
plt.xlabel('Value')
plt.ylabel('Frequency')
# Show the plot
plt.show()
观察到
var
特征是正态分布的,其中均值和中值(50% 百分位数)预计大致相等。 对于倾斜分布,均值倾向于向更重的尾部倾斜。
然而,这些是启发式检查,实际确定使用Shapiro-Wilk测试或Kolmogorov-Smirnov正态性测试等特定统计测试来完成。
二项分布
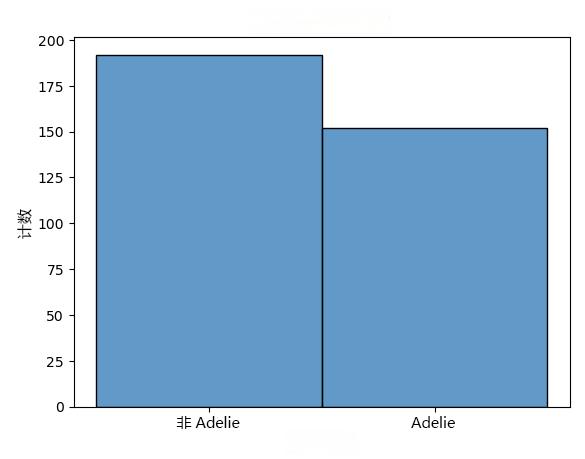
假设你想了解在一群企鹅中观察到的特定特征有多好。
你决定检查一个包含 200 只企鹅的数据集,看看它们是否属于阿德尔物种。这是一个二项分布问题,因为有两种可能的结果(是或不是阿德尔物种)、试验数是固定的(200 只企鹅),并且每个试验都与其他试验独立。
分析数据集后,你发现有150 只企鹅属于阿德尔物种。
知道数据遵循二项分布,就可以对将来的企鹅数据集或企鹅组进行预测。 例如,如果你研究另一组 200 只企鹅,可以预计大约 150 只企鹅是阿德利企鹅。
以下 Python 代码绘制了
is_adelie
二项变量的直方图。
sns.histplot
中的
discrete=True
可确保将 bin 视为离散间隔。 这意味着直方图中的每个条与一个类别或布尔值完全对应,从而使绘图更容易解释。
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
# Load the Penguins dataset from seaborn
penguins = sns.load_dataset('penguins')
# Create a binomial variable for 'species'
penguins['is_adelie'] = np.where(penguins['species'] == 'Adelie', 1, 0)
# Plot the distribution of 'is_adelie'
sns.histplot(data=penguins, x='is_adelie', bins=2, discrete=True)
plt.title('Binomial Distribution of Species')
plt.xticks([0, 1], ['Not Adelie', 'Adelie'])
plt.show()
均匀分布
均匀分布(也称为矩形分布)是一种概率分布,其中所有结果的概率都是相等的。 在分布的支撑点上,每个长度相同的间隔具有相同的概率。
import numpy as np
import matplotlib.pyplot as plt
# Generate a uniform distribution
uniform_data = np.random.uniform(-1, 1, 1000)
# Plot the distribution
plt.hist(uniform_data, bins=20, density=True)
plt.title('Uniform Distribution')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()
在此代码中,
np.random.uniform
函数生成 1000 个随机数,这些随机数在 -1 和 1 之间均匀分布。
bins=30
参数指定应将数据划分为 30 个 bin,并且
density=True
确保将直方图归一化来形成概率密度。 这意味着直方图下方的面积总和为 1,这在比较分布时很有用。
注意
如果多次运行代码,可能会获得不同的结果。 随机性的基本思想是,它是不可预测的,并且每次采样时,都可获得不同的结果。
可使用
np.random.seed
设置种子值来控制此过程。这对于在模型构建阶段测试和调试非常有用,因为它允许重现相同的结果。