资讯

历史

科技

环境与自然

成长

游戏

财经

文学与艺术

美食

健康

家居

文化

情感

汽车

三农

军事

旅行

运动

教育

生活

星座命理

弹性网络回归（Elastic Net）详解：L1与L2正则化的完美平衡

创作时间:

作者:

@小白创作中心

弹性网络回归（Elastic Net）详解：L1与L2正则化的完美平衡

引用

CSDN

https://blog.csdn.net/maoyu_dual/article/details/146136397

弹性网络回归（Elastic Net）简介

在机器学习的回归分析领域，弹性网络（Elastic Net）作为一种强大的线性回归技术，是岭回归（L2正则化）与Lasso回归（L1正则化）的融合版本。这种融合并非简单的叠加，而是为了解决两类回归方法在实际应用中所面临的局限性。

Lasso回归的局限性

当特征之间存在高度相关性时，Lasso回归会面临一个棘手的问题：它倾向于随机选择其中一个相关特征，而忽略其他相关特征。这一特性使得Lasso回归在处理高度相关特征时，模型的稳定性大打折扣。例如，在金融风控场景中，如果收入和负债这两个高度相关的特征同时存在，Lasso可能只会随机选择其中一个，从而导致模型无法全面考虑相关因素，影响预测的准确性。

岭回归的冗余性

与Lasso回归不同，岭回归会保留所有的特征，无论这些特征是否对目标变量有显著影响。虽然这种方法可以保证模型的稳定性，但却无法有效地筛选出关键变量，导致模型可能包含大量冗余信息，增加了模型的复杂度和计算成本。

弹性网络的核心优势

弹性网络结合了Lasso和岭回归的优点，在特征高度相关时能够稳定地选择变量。它通过双重正则化，实现了特征选择与权重收缩的平衡。具体来说，弹性网络的双重正则化机制使得它既能像Lasso一样进行特征选择，又能像岭回归一样保证模型的稳定性。这种平衡使得弹性网络在处理复杂数据集时表现出色，尤其适用于特征高度相关且需要稀疏解的场景。

数学原理与优化方法

目标函数

弹性网络的损失函数结合了L1和L2正则化项，其数学表达式如下：

[
\text{Loss} = \frac{1}{2N} |\mathbf{y} - \mathbf{X}\mathbf{w}|_2^2 + \lambda \left( \rho |\mathbf{w}|_1 + \frac{1-\rho}{2} |\mathbf{w}|_2^2 \right)
]

在这个公式中，各个参数具有重要的意义：

$\lambda$ 控制整体正则化强度。$\lambda$ 值越大，正则化的效果越强，模型越简单，对特征的约束也越大。例如，当$\lambda$ 趋近于无穷大时，所有的特征权重都将趋近于零，模型将变得非常简单。
$\rho$（l1_ratio）调节L1与L2的权重。当 $\rho=1$ 时，弹性网络退化为Lasso回归；当 $\rho=0$ 时，弹性网络退化为岭回归。通过调整$\rho$ 的值，我们可以在L1和L2正则化之间找到一个合适的平衡点。

优化：坐标下降法

与Lasso回归类似，弹性网络使用坐标下降法逐维度更新权重。这种方法的核心思想是在每次迭代中，固定其他维度的权重，只更新一个维度的权重。在弹性网络中，由于需要同时处理L1和L2正则化项，权重更新公式变得更加复杂：

[
w_j = \frac{S\left( \sum_{i=1}^N x_{ij}(y_i - \tilde{y}i^{(j)}) , \lambda \rho \right)}{\sum{i=1}^N x_{ij}^2 + \lambda (1-\rho)}
]

其中 $S(\cdot)$ 是软阈值函数，分母中的 $\lambda(1-\rho)$ 项来自L2正则化。坐标下降法的优点是计算复杂度较低，尤其适用于高维数据集。

超参数调优：λ与ρ的选择

参数作用

λ（alpha）：整体正则化强度。$\lambda$ 越大，模型越简单，对特征的约束越强。在实际应用中，我们需要根据数据集的复杂度和样本数量来选择合适的$\lambda$ 值。如果数据集比较复杂，包含大量的特征和噪声，我们可以选择较大的$\lambda$ 值来防止过拟合；如果数据集比较简单，我们可以选择较小的$\lambda$ 值来提高模型的拟合能力。
ρ（l1_ratio）：L1正则化的比例。$\rho$ 越接近1，特征选择越激进，模型越倾向于选择较少的特征；$\rho$ 越接近0，模型越倾向于保留所有的特征，类似于岭回归。

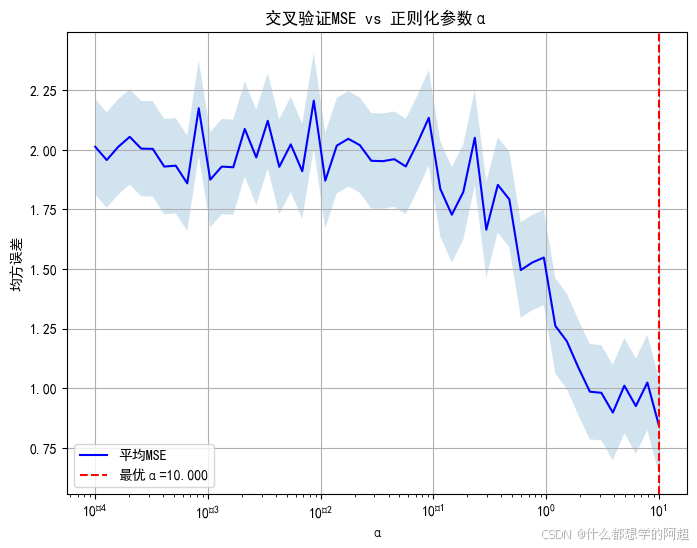
网格搜索与交叉验证

在实际应用中，我们通常使用网格搜索结合交叉验证的方法来选择最优的$\lambda$ 和$\rho$ 值。Scikit-Learn提供了ElasticNetCV类来自动化这个过程。以下是一个示例代码：

from sklearn.linear_model import ElasticNetCV
import numpy as np

# 生成具有相关特征的数据
X = np.random.randn(100, 10)
X[:, 2] = X[:, 1] + np.random.normal(0, 0.1, 100)  # 特征1和2高度相关
y = 3 * X[:, 1] + 2 * X[:, 5] + np.random.randn(100)

# 定义参数范围
l1_ratios = [0.1, 0.5, 0.7, 0.9, 0.95, 1]
alphas = np.logspace(-4, 2, 50)

# 交叉验证选择最优参数
model = ElasticNetCV(l1_ratio=l1_ratios, alphas=alphas, cv=5, max_iter=10000)
model.fit(X, y)
print("最优λ:", model.alpha_)          # 示例输出：0.05
print("最优ρ:", model.l1_ratio_)      # 示例输出：0.7

代码实战：金融风控变量筛选

数据集：借款人信用数据

在金融风控领域，我们通常需要根据借款人的各种信息来预测贷款违约概率。假设我们有一个包含20个特征的数据集，这些特征包括年龄、收入、负债比、历史逾期次数等，其中有5个特征是强相关的。我们的目标是预测贷款违约概率，这是一个连续值。

![](https://wy-static.wenxiaobai.com/chat-rag-image/13936165324117864337)

from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler

# 生成模拟数据（5个有效特征，其中3个高度相关）
X, y, coef = make_regression(n_samples=500, n_features=20, n_informative=5, 
                             noise=15, coef=True, random_state=42)
X[:, 1] = X[:, 0] + np.random.normal(0, 0.3, 500)  # 特征0和1相关
X[:, 2] = X[:, 0] * 0.8 + np.random.normal(0, 0.2, 500)

# 标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

模型训练与权重分析

from sklearn.linear_model import ElasticNet
import matplotlib.pyplot as plt

# 训练弹性网络（使用最优参数）
enet = ElasticNet(alpha=0.05, l1_ratio=0.7)
enet.fit(X_scaled, y)

# 获取非零权重
selected_features = np.where(enet.coef_ != 0)[0]
print("筛选后的特征索引:", selected_features)  # 示例输出：[0,1,2,5,7]

# 对比真实权重
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.stem(coef, markerfmt='bo', label="真实权重")
plt.title("真实权重分布")
plt.subplot(1, 2, 2)
plt.stem(enet.coef_, markerfmt='ro', label="弹性网络估计")
plt.title("弹性网络权重")
plt.tight_layout()
plt.show()

结论：弹性网络保留了相关特征（0,1,2），而Lasso可能只选择其中一个。这说明弹性网络在处理高度相关特征时具有更好的稳定性和特征选择能力。

应用场景与局限性

适用场景

金融风控：在金融领域，弹性网络可以用于筛选强相关指标，如收入与负债组合。通过选择合适的特征，我们可以提高贷款违约概率预测的准确性，降低风险。
生物信息学：在生物信息学中，基因表达数据通常存在共线性问题。弹性网络可以有效地处理这些共线性问题，帮助研究人员筛选出关键基因，提高疾病诊断和治疗的效果。
推荐系统：在推荐系统中，用户的行为数据往往非常庞大，包含大量的特征。弹性网络可以从海量用户行为中提取关键特征，提高推荐的准确性和效率。