有限域、伽罗华域、Galois Fields、GF

有限域、伽罗华域、Galois Fields、GF

引用

CSDN

1.

https://blog.csdn.net/xiangsimoyinjiu/article/details/143225728

有限域（Galois Fields，简称GF）是密码学中的一个重要概念，它在保证数据安全传输方面发挥着关键作用。本文将从整数域出发，逐步介绍有限域的定义、特点以及在加法、减法和乘法运算中的具体实现方式。

域

一个可以进行加减乘除的集合，而且结果都在集合中。最简单的整数域中，例如：

• 1 + 2 = 3
• 2 + 1 = 3
• 2 * 3 = 6
• 6 / 3 = 2

这个域有个特点，只要知道两个元素和它们的运算类型，就可以知道他们的结果，知道其中一个元素、结果和运算类型，也可以反推另一个元素。

密码学中，如果想发送一个数字2，直接发送会被别人知道。可以将2加密为6，并约定接收方收到数据后除以3就是原始数字。加密过程为2 * 3 = 6，解密过程为6 / 3 = 2。为了增加加密的可靠性，可以将加密步骤复杂化。例如，想发送0123，可以产生一个伪随机数列2835，然后相加，发送2958。只要增加伪随机数列的长度和运算复杂度，就能增加破解难度。

但整数域是无限的，例如想发送8，乘以3就是24，这样加密后长度就增加了，影响传输速度且不利于解密。如果这个域有有限个元素就好了，这就是有限域。

有限域

也称伽罗华域（Galois Fields），简称GF，集合中有有限个元素，集合中的元素加减乘除，结果都在集合中。

加法

以GF(2^4)为例，里面有0-15总共16个数。先说加法，10 + 6 = 16溢出怎么办？对16取余数，这样15+1=16%16=0，0-1=0-1+16=15，这样加减法就闭环了，任何两个数相加减，结果还在这个集合里。但对于计算机而言，数是以二进制的形式储存的，所以15+1计算机是这样算的：

这样的加法有个缺点，有进位，想得到最高位的结果必须等到次高位计算完成，必须从最低位到最高位开始算，高位要等低位的计算结果，这样对于计算机来说加密的效率太低了，最好能并行运算，每一位同时进行计算，这样不管数有多大，有多少位，算加法只要一个时间单位。

简化一下问题，单独看0和1加法的各种情况：

其实问题就出现在1+1了，只有这种情况会出现溢出，那我就定义1+1=0,为什么不定义1+1=1？如果这样定义，1+1和0+1都是1，那1-1是等于0还是1？也就是不可逆了。然后我们发现这其实就是异或操作（如果两个数相同，则结果为0，不同则为1），计算机实现这个非常方便，而且再看减法，也是异或，所以加减法是一样的，非常好！！！

A + B = A − B = A ⨁ B

而且只要知道其中任意两个数，异或以后就可以得到第三个数：

A ⨁ B = C , B ⨁ A = C

C ⨁ A = B , C ⨁ B = A

C ⨁ B = A , C ⨁ A = B

这样不管多大的两个数相加减，就是按位异或，可位之间互不影响，可并行运算，效率非常高。

GF(n) 的加减法代码如下：

print('|aa')
n = 16
data = []
for i in range(n):
    data.append([0] * n)
for i in range(n):
    for j in range(n):
        data[i][j] = i ^ j
s = '+/- '
for i in range(n):
    s = s + ('%4d' % i)
s = s + '\n'
for i in range(n):
    s = s + ('%4d' % i)
    for j in range(n):
        s = s + ('%4d' % data[i][j])
    s = s + '\n'
print(s)

GF(2^2)的加减法表如下：

• 每一列，每一行除了开始都不相同，说明运算是可逆的，可以通过其中两个数推导出第三个数
• 整个表沿着斜对角对称，说明运算是可交换的

GF(2^4)的加减法表如下：

乘法

再看乘法，5x7，注意加减都是异或，写成二进制，乘法就是移位和加法（异或），移位操作对于计算机来说也比较容易。5x7=27，溢出了，用同样的方法对16取余数，那5x7=27%16=11。那2x9呢？2x9=18%16=1_0010 XOR 1_0000=2，2x1=2, 2/2等于1还是9？？？不可逆！！！如果17呢？4x5=20%17=1_0100 XOR 1_0001 = 5，1x5=5，也不行18呢? 2x9=18%10=0,2x0=0，可见偶数绝对不行如果溢出后对19取余数呢？

可以看出：

2^4 = 16 mod 19 =16 - 19 =16 ⨁ 19 = 3

如果乘法产生出2^5呢？那将19也左移一位：

48 = 2^5 ⨁ 2^4=2^5 ⨁ 3=5

2^5 = 5 ⨁ 3 = 6 = 3 << 1 = 2^4 << 1

按照这个算下去，会发现很有趣的结果：

A B C

0 0000 0

2^0 0001 1

2^1 0010 2

2^2 0100 4

2^3 1000 8

2^4 0011 3

2^5 0110 6

2^6 1100 12

2^7 1011 11

2^8 0101 5

2^9 1010 10

2^10 0111 7

2^11 1110 14

2^12 1111 15

2^13 1101 13

2^14 1001 9

2^15 0001 1

2^n就表示将0001做n次以下的操作，如果左移没有溢出，则不需要取余数

( 0001 << 1 ) ( ? mod 10011 )

而这样做了15次后这个数会变回自己，对于A=1,2,3…,15

[ ( ( A << 1 ) ( ？ mod 10011 ) ] * 15 = A

而且刚好一一对应了1-15

那么乘法可以这样定义，GF(2^4)中任何数乘以0等于0，任何非零数相乘：

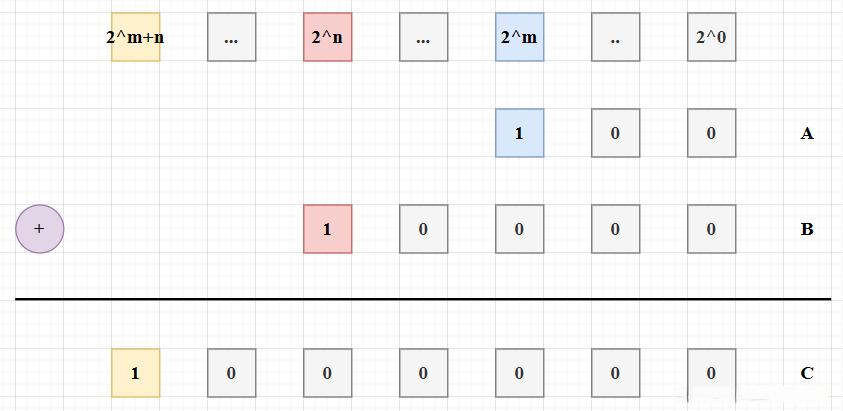
A ∗ B = 2^m * 2^n=2^{(m+n)mod16}

列一下乘法表：

• 对称 => 可交换
• 每行每列都不同 => 可逆

import galois
![](https://wy-static.wenxiaobai.com/chat-rag-image/3917355990749672308)
GF = galois.GF(2 ** 4, irreducible_poly = "x^4 + x + 1")
print('|aa')
n = 16
data = []
def GFPlus(a, b):
    c = 0
    for i in range(4):
        if (1 << i) & a:
            c = c ^ (b << i)
    for i in [7, 6, 5, 4]:
        if (1 << i) & c:
            c = c ^ (19 << (i - 4))
    # print(a,b,c)
    return c
for i in range(n):
    data.append([0] * n)
for i in range(n):
    for j in range(n):
        data[i][j] = GFPlus(i, j)
s = '   *'
for i in range(n):
    s = s + ('%4d' % i)
s = s + '\n'
for i in range(n):
    s = s + ('%4d' % i)
    for j in range(n):
        s = s + ('%4d' % data[i][j])
    s = s + '\n'
print(s)
def checkData(s):
    if (len(list(set(s))) != len(s)):
        print('Error: repeat')
    else:
        # print('Success')
        return True
for i in range(15):
    checkData(data[i+1])
    checkData(data[:][i+1])