点估计:矩估计 & 极大似然估计
点估计:矩估计 & 极大似然估计
在统计学中,点估计是一种重要的参数估计方法,它通过样本数据来估计总体参数的值。本文将介绍两种常用的点估计方法:矩估计和极大似然估计,并通过具体例子帮助读者理解它们的原理和应用。
估计问题与检验问题,作为发展最成熟的问题,是统计推断的两大支柱。
一个最简单的估计命题可以是,由样本X算出一个值,作为均值a的估计,这个估计被称作点估计(point estimation)。
假设上班族中有3个人,他们每个月的零用钱分别为3000元、4000元、5000元,如何根据这些信息估计所有上班族的零用钱水平呢?求平均值就是一种方法,这个数值是固定的、明确的。点估计的第一目标就是寻求类似平均值的估计量,最优地表达数据的特点。
在算法领域里有一条极其重要的原则:NFL(天下没有免费的午餐,No Free Lunch)。NFL是说,脱离具体的问题或场景,空谈哪种算法更好毫无意义。也就是说,不存在一个绝对最优的估计量。我们只能基于某个特殊的场景,从某个特定角度出发,寻找具备最优性质的估计量。
于是,在点估计问题中,从不同的角度出发寻找最优解就出现了两大类常用方法:其一是广泛使用的矩估计(moment estimation);其二是名气更大的极大似然估计(Maximum Likelihood Estimation,MLE)。
矩估计

卡尔·皮尔逊 (Karl Pearson 1857~1936)
矩估计的发源要追溯到1894年,它是在K. Pearson描述生物学数据的基础上发展而来的。“矩”的概念让我们想起了经典物理学中表示距离和物理量相乘的物理量,如果用“点”表示“质量”,则零阶矩表示总质量,一阶矩表示重心,二阶矩表示转动惯量……
因此,物理学中的“矩”描述的是物质的空间分布情况,而统计学中的“矩”描述的则是随机变量的分布情况。
也就是说,如果用“点”来表示“概率密度”(概率密度可以告诉我们随机变量取某些特定值的概率),那么在数学上可以通过求“和”(对于离散变量是相加,对于连续变量是求积分)创造出一系列统计学中的矩概念:
零阶矩:总概率,即概率的和一定等于1,所有随机变量的零阶矩都是一样的。
一阶矩:分布的数学期望(均值),衡量随机变量到原点的距离。
二阶矩:可以用来计算方差,衡量分布的数据的离散程度。
三阶矩:偏度(skewness),衡量分布的随机密度函数向左或向右偏的程度。
四阶矩:峰度(kurtosis),衡量分布的峰部有多尖(尽管从数学本质上来说,它更适合描述分布尾部的大小)。
概率密度函数与矩之间的这种密切的联系,深耕于数学的美学形式之中。如果你了解泰勒级数,就能很好地理解矩的分布意义。泰勒级数是分级的,可以用来描述函数的特征;矩是分阶的,可以用来表达概率密度函数的形状和特征。
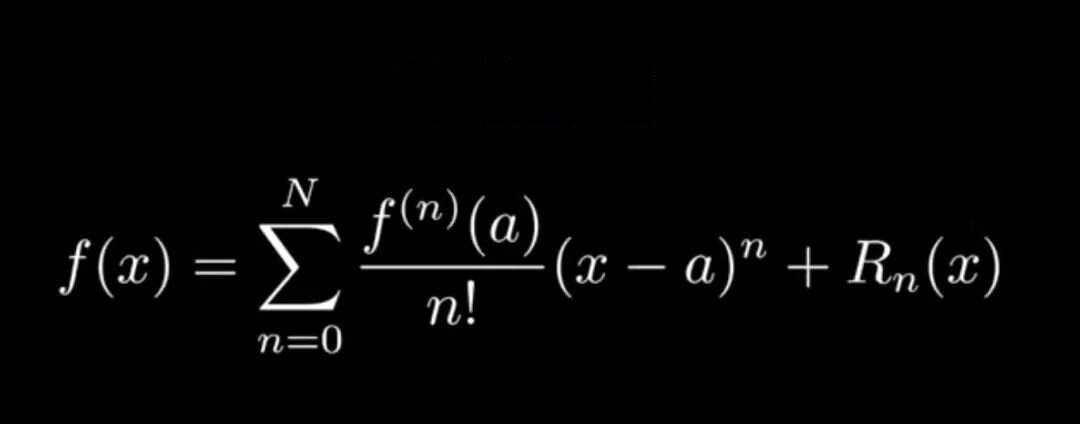
例如,知道了均值,就相当于知道了泰勒级数中的f(0);知道了方差(结果的离散程度),就相当于知道了泰勒级数f(0)的导数f'(0)(f变化得有多快)。泰勒级数有更多的级数就意味着有更多关于函数的信息。矩也是如此,信息越多,对概率密度函数的近似就越好。
下面来看一系列概率密度函数的矩信息。
对于正态分布,四个阶的矩都存在,其三阶矩为0,四阶矩为3。
对于标准均匀分布,四个阶的矩都存在,其四阶矩为1.8。
对于偏态的Pareto分布80/20,存在一阶矩,但二阶及以上的矩不存在。
对于部分幂律分布,只有一阶矩和二阶矩,三阶及以上的矩不存在。
对于所有的分布而言,其前两个矩(如均值和方差)是目前已知的最关键的两个矩。虽然所有的矩都很重要,但有些矩比其他矩更加重要。在这里,对于二阶矩的理解,我们需要耐心一些,尽管二阶矩可以用来计算方差,但二阶矩并不是方差。
真正的方差的计算方法是先从所有的值中减去均值,再进行平方,因此方差往往被称为二阶中心矩,而不是二阶矩。更准确的说法应该是,方差(二阶中心矩)= 二阶矩 - 一阶矩的平方:
Var(X)=E(X²)-E(X)²
这是一个更加简单的计算方差的公式,省掉了方差公式中烦琐的减法运算。在数学上能够这样简化的深层原因在于,求和与求积分都是线性运算。
了解了矩的概念,就可以继续对矩进行估计,这就是矩估计,即利用样本自身的矩来估计样本总体的相应参数。
弱大数定理告诉我们,简单随机样本的一阶矩按概率收敛到相应的总体一阶矩。
这就启发我们,可以用样本矩替换总体矩,进而找出未知参数的估计。进一步地,如果总体的概率密度函数中有k个未知矩参数,就可以用样本的前k阶矩来估计总体的前k阶矩,利用未知参数与总体矩的函数关系求出参数的估计量。换句话说,由矩的概念引申出了独立的概率密度函数的估计方法。
例如,我们用样本的一阶原点矩来估计总体的数学期望,用样本的二阶中心矩来估计总体的方差等。
就像泰勒级数一样,由于只通过有限的矩的数学特征来得到参数的估计量,不会探求一个分布的概率密度函数的精确表达,精确表达的程度只与矩的信息多少相关,因此矩估计方法并不会用到总体的分布模型。这意味着,矩估计使用起来很简单。
极大似然估计
费希尔(Sir Ronald Fisher 1890~1962)
当然,矩估计的这一特点也招致了理论家的批判。英国统计学家Fisher就认为矩估计法并不是一个无懈可击的方法,短估计法没有最大程度整合样本里的信息,这种浪费是一个巨大的缺憾。Fisher的一生对矩估计有着深深的敌意,这一思想的根源是他更多地从“估计方法能整合样本里的多少信息”的角度去思考问题。
这一思考角度在统计学发展的历史上意义重大,并引发了一系列连锁反应。一方面,带来了“充分统计量”的概念。另一方面,Fisher与天文学家爱丁顿起了争论,并严肃地探讨了平均绝对偏差和标准差哪个估计量更好的话题。
站在批判矩估计的立场上,Fisher自然需要给出他的候选答案。Fisher认为,统计模型的选择需要结合实际情况考虑,而不能像矩估计一样进行单纯的数学求解。这就是1912年Fisher正式提出极大似然估计的历史背景。
那么,什么是极大似然估计呢?下面不妨来看一个投掷图钉的例子。
假设有一枚图钉,设p为随机投掷后图钉针尖朝上的概率,现求p。显然,这个问题要求我们做实验,并通过观察求取概率p的估计值。
实验开始,假设我们投掷图钉5次,图钉针尖朝向结果为上、下、上、上、下,即3次朝上,2次朝下。在5次实验互不影响的前提下,图钉针尖朝向顺序出现的概率y可以写成:
y=p³(1-p)²
这个方程还被称作似然函数。画出这个似然函数的图像,我们能够很轻易地捕捉到似然函数有一个局部极大值点。
通过求解y'=0可知,当p=0.6时(C点),似然函数y取到局部极大值。这种将p的估计值设定为一个值,使y取到局部极大值的基本思想就是极大似然估计。这个p值就是图钉针尖朝上的概率估计值,利用这个值能够完美地解释实验的结果。
简单来说,极大似然估计的逻辑就是,猎人和徒弟去打猎,打到了一只兔子,猜一猜更有可能是谁打到的?为了回答这个问题,你至少要对猎人和徒弟的狩猎能力(模型)都有所了解,并给出自己的判断。
显然,极大似然估计与矩估计的思路是决然不同的。前者在选定模型之后,再进行参数估计,而不像矩估计一样,不管模型到底是什么,都先进行参数估计。这就是Fisher的极大似然估计与Pearson的矩估计的最大区别。
Fisher的观点几乎完全排斥矩估计,并努力寻找全新的工具。这样的冲突让极大似然估计的思想独立发展起来并自成一派。