深度学习中的微积分基础:导数、梯度、链式法则与偏导数详解
深度学习中的微积分基础:导数、梯度、链式法则与偏导数详解
深度学习的核心在于优化模型参数以最小化损失函数,而微积分中的导数、梯度、链式法则和偏导数等概念是实现这一目标的关键工具。本文将详细阐述这些数学概念在深度学习中的具体应用,并通过代码示例帮助读者加深理解。
前言
在深度学习中,微积分是理解和优化模型的核心工具。微积分中的基本概念,如导数、梯度、链式法则和偏导数,是训练神经网络时进行反向传播和优化的基础。以下将详细论述这些基本概念,并附带相关的公式和代码示例,帮助加深理解。
1. 导数(Derivative)
1.1 导数的定义
导数表示函数在某一点的瞬时变化率。对于一个标量函数f ( x ) f(x)f(x),导数f ′ ( x ) f′(x)f′(x)给出了函数在点x xx处的切线斜率,反映了函数输出随输入变化的敏感度。
1.2 导数在深度学习中的应用
在神经网络训练过程中,我们需要通过优化损失函数来调整模型的权重。为此,必须计算损失函数相对于各个权重的导数。导数帮助我们理解损失函数对权重的变化如何影响模型的输出,并指导我们通过梯度下降法来更新模型的参数。
- 代码示例:计算函数的导数
import sympy as sp
# 定义符号变量
x = sp.symbols('x')
# 定义函数 f(x) = x^2 + 3x + 2
f = x**2 + 3*x + 2
# 计算 f(x) 的导数
dfdx = sp.diff(f, x)
print("导数:", dfdx)
2. 梯度(Gradient)
2.1 梯度的定义
梯度是一个向量,包含了函数对每个输入变量的偏导数。对于一个多变量函数f ( x 1 , x 2 , . . . , x n ) f(x1,x2,...,xn)f(x1,x2,...,xn),梯度是一个由所有偏导数组成的向量:
2.2 梯度在深度学习中的应用
梯度在深度学习中用于优化算法。反向传播算法通过计算损失函数的梯度,告诉我们如何调整每个参数(权重)以最小化损失函数。梯度下降法通过沿着梯度的反方向更新权重,从而使得损失函数逐渐减小。
- 代码示例:计算梯度
import numpy as np
# 定义一个函数 f(x) = x^2 + 3x + 2
def f(x):
return x**2 + 3*x + 2
# 定义梯度函数
def gradient_f(x):
return 2*x + 3
# 计算梯度
x_value = 2
grad = gradient_f(x_value)
print(f"在 x = {x_value} 处的梯度是:", grad)
3. 链式法则(Chain Rule)
3.1 链式法则的定义
链式法则是微积分中用于复合函数求导的规则。如果有两个函数y = g ( u ) y=g(u)y=g(u)和u = f ( x ) u=f(x)u=f(x),那么y yy关于x xx的导数可以表示为:
在深度学习中,链式法则用来计算复杂神经网络中损失函数对各层参数的导数。反向传播算法利用链式法则从输出层开始,逐层向前传播误差并更新权重。
3.2 链式法则在深度学习中的应用
假设有一个由多个层组成的神经网络,每一层的输出都依赖于上一层的输出。链式法则帮助我们计算损失函数相对于每个权重的梯度。
- 代码示例:使用链式法则计算复合函数的导数
# 定义复合函数 f(x) = sin(x^2)
def f(x):
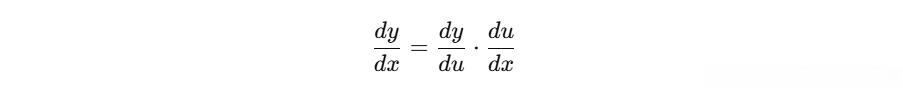
return np.sin(x**2)
# 定义内外层的导数
def df_dx(x):
return 2*x * np.cos(x**2)
# 计算导数
x_value = 3
derivative = df_dx(x_value)
print(f"在 x = {x_value} 处的导数是:", derivative)
4. 偏导数(Partial Derivative)
4.1 偏导数的定义
偏导数是多元函数中,针对某一个变量求导时,其他变量保持不变的情况下的导数。对于一个函数f ( x 1 , x 2 , . . . , x n ) f(x1,x2,...,xn)f(x1,x2,...,xn),偏导数是对某个特定变量(比如x 1 x1x1)求导,其它变量不变:
4.2 偏导数在深度学习中的应用
在深度学习中,神经网络的损失函数通常是关于多个参数的函数。通过计算损失函数相对于每个参数的偏导数,我们能够知道如何更新每个参数以最小化损失。偏导数是反向传播算法的核心。
- 代码示例:计算偏导数
import sympy as sp
# 定义符号变量
x, y = sp.symbols('x y')
# 定义多元函数 f(x, y) = x^2 + y^2
f = x**2 + y**2
# 计算 f(x, y) 对 x 的偏导数
partial_derivative_x = sp.diff(f, x)
print("对 x 的偏导数:", partial_derivative_x)
# 计算 f(x, y) 对 y 的偏导数
partial_derivative_y = sp.diff(f, y)
print("对 y 的偏导数:", partial_derivative_y)
5. 反向传播与优化
反向传播是利用梯度下降法优化神经网络的核心算法。它依赖于链式法则和梯度计算,通过在每一层传播误差来更新权重。反向传播过程可以概括为:
- 前向传播:计算每层的输出,最终得到损失函数。
- 计算梯度:根据损失函数对每一层的输出和权重进行梯度计算。
- 反向传播:使用链式法则将梯度从输出层反向传播到每一层。
- 更新权重:利用梯度下降法(或其他优化算法)更新每个权重。
5.1 梯度下降
梯度下降是一种常见的优化算法,通过沿着损失函数的梯度方向更新模型参数,以最小化损失函数。
更新规则为:
其中,θ θθ是参数,α αα是学习率,∇ θ J ( θ ) ∇_θJ(θ)∇θ J(θ)是参数θ θθ的梯度。
- 代码示例:梯度下降算法
import numpy as np
# 定义损失函数 J(theta) = (theta - 3)^2
def loss_function(theta):
return (theta - 3)**2
# 定义梯度
def gradient(theta):
return 2 * (theta - 3)
# 梯度下降
theta = 0 # 初始化参数
learning_rate = 0.1
epochs = 100
for epoch in range(epochs):
grad = gradient(theta)
theta = theta - learning_rate * grad # 更新参数
if epoch % 10 == 0:
print(f"Epoch {epoch}, theta: {theta:.4f}, loss: {loss_function(theta):.4f}")
总结
微积分是深度学习中优化过程的核心工具。通过计算导数、梯度、偏导数以及使用链式法则,我们能够有效地通过反向传播算法调整神经网络的参数,使得损失函数逐步减少。微积分不仅有助于理解神经网络的训练过程,也为优化算法(如梯度下降法)提供了理论依据。