Lasso回归（L1正则化回归）详解：从原理到实战

Lasso回归（L1正则化回归）详解：从原理到实战

引用

CSDN

1.

https://blog.csdn.net/maoyu_dual/article/details/145966766

Lasso回归（Least Absolute Shrinkage and Selection Operator）是机器学习领域中一种重要的线性回归算法，它通过L1正则化实现特征选择和模型简化。本文将从基本概念、数学原理、优化方法、代码实现等多个维度，深入解析Lasso回归的工作原理及其应用场景。

1. Lasso回归：稀疏性与特征选择

Lasso回归作为线性回归的L1正则化版本，在机器学习领域中占据着重要的地位。它的核心优势在于能够同时实现两个关键目标：

1.1 特征选择

在许多实际问题中，数据往往包含大量的特征，但并非所有特征都对目标变量有显著的影响。Lasso回归能够自动筛选出重要特征，其原理是通过将不相关特征的权重设为0，从而简化模型结构，提高模型的可解释性和计算效率。例如，在基因表达数据中，可能有成千上万个基因的表达水平作为特征，但只有少数基因与特定的疾病或生理过程相关。Lasso回归可以帮助我们从这些海量的特征中找出真正有意义的基因。

1.2 正则化

过拟合是机器学习中一个常见的问题，特别是当模型的复杂度较高时。Lasso回归通过收缩权重，即对权重进行惩罚，有效地防止了过拟合的发生。这种正则化机制使得模型在训练数据上不会过度拟合，从而提高了模型的泛化能力。

1.3 适用场景

• 高维数据：当特征数远远大于样本数时，如基因表达数据，传统的线性回归方法可能会因为过拟合而失效。Lasso回归通过特征选择和正则化，能够在高维数据中找到一个简单而有效的模型。
• 需要模型可解释性的场景：在一些领域，如金融风控，我们不仅需要预测结果，还需要理解模型是如何做出决策的。Lasso回归通过将不相关特征的权重设为0，使得模型更加简洁，易于解释。

2. 数学推导与几何解释

2.1 目标函数

Lasso回归的目标函数是在均方误差（MSE）的基础上增加了L1正则化项，其数学表达式为：

其中，(|\mathbf{y} - \mathbf{X}\mathbf{w}|_2^2) 是均方误差，表示模型的预测值与真实值之间的差异；(\lambda) 是正则化参数，用于控制正则化的强度；(|\mathbf{w}|1 = \sum{j=1}^n |w_j|) 是L1范数，表示权重向量的绝对值之和。

2.2 几何解释：菱形约束与角点解

• 无正则化：在没有正则化的情况下，线性回归的解位于均方误差等高线的中心，此时模型的权重可以取任意值，以最小化均方误差。
• L1正则化：当引入L1正则化后，约束区域变成了一个菱形。由于L1范数的性质，最优解通常出现在坐标轴上，即某些权重为0。这就是Lasso回归能够实现特征选择的几何原理。

2.3 Lasso回归的核心概念可视化

为了更好地理解Lasso回归的工作原理，我们通过以下四个图来直观展示其关键概念：

L1正则化的几何解释：展示了二维特征空间中的L1约束（红色虚线菱形）与L2约束（蓝色虚线圆）的对比。L1约束的菱形形状使得最优解更容易出现在坐标轴上，这就是Lasso能够产生稀疏解的几何原因。

Lasso路径图：展示了随着正则化参数λ的变化，不同特征权重的变化趋势：

• 当λ较大时，所有权重趋近于0
• 随着λ减小，重要特征的权重逐渐显现
• 不重要的特征权重始终保持为0，体现了特征选择的效果

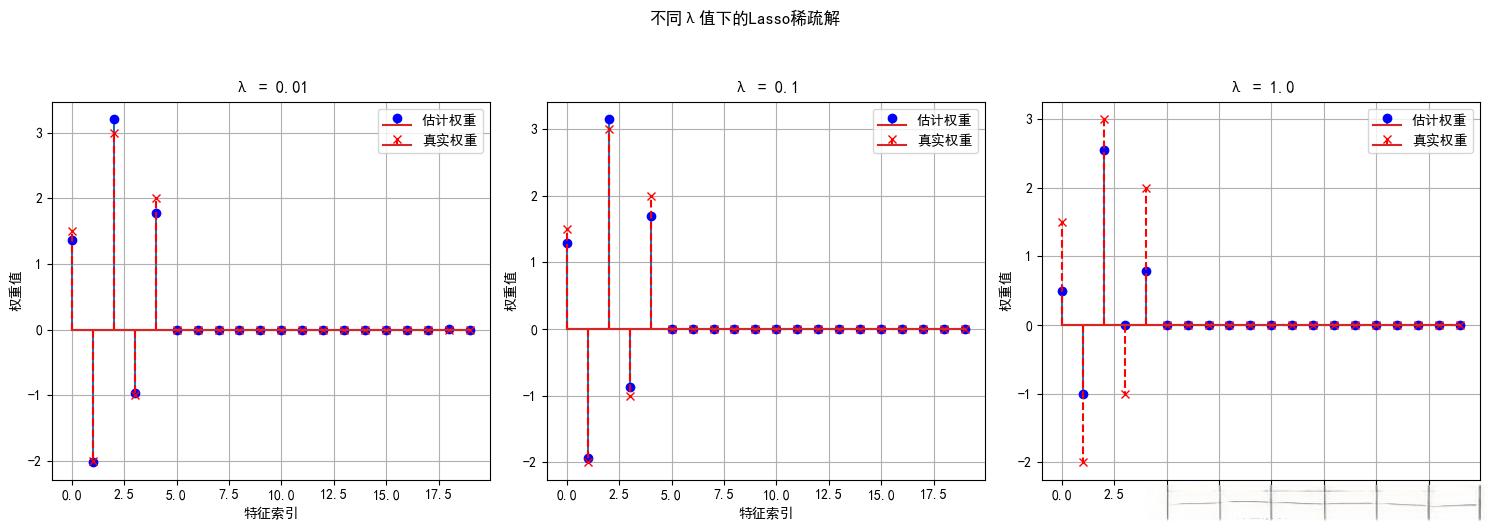
特征选择效果：直观展示了Lasso的特征选择能力：

• 蓝色点表示模型估计的权重
• 红色叉表示真实的权重
• 可以看到Lasso成功识别出了真正重要的特征，将其他特征的权重压缩为0

交叉验证选择λ：展示了如何通过交叉验证选择最优的正则化参数λ：

• 黑线表示平均MSE随λ的变化
• 灰色区域表示MSE的标准差范围
• 红色虚线标记了最优的λ值，在该点处模型达到最佳性能

这些可视化帮助我们更直观地理解Lasso回归的工作原理，特别是其特征选择机制和正则化效果。

3. 坐标下降法优化原理

由于L1正则项在某些点处不可导，传统的梯度下降方法不再适用。因此，我们需要使用一种特殊的优化方法——坐标下降法。坐标下降法通过逐个维度优化权重，逐步逼近最优解。

3.1 单变量闭式解

3.2 坐标下降法的可视化解释

为了更好地理解坐标下降法的工作原理，我们通过以下三个图来直观展示其关键概念：

优化过程：展示了二维空间中的坐标下降优化过程：

• 等高线表示目标函数的损失值
• 红色箭头表示优化路径，每次只沿一个坐标轴方向移动
• 最终收敛到最优解（红色星号标记）

软阈值函数：展示了坐标下降法中使用的软阈值函数：

• 虚线表示原始值
• 红线表示经过软阈值处理后的值
• 绿色虚线表示阈值λ的位置
• 当输入值的绝对值小于λ时，输出被压缩为0

单维度优化：展示了单个维度上的优化过程：

• 蓝色虚线表示均方误差项
• 绿色虚线表示L1正则项
• 红色实线表示总损失函数
• 黑色虚线表示该维度的最优解

这些可视化帮助我们理解坐标下降法如何在每个维度上独立优化，以及软阈值函数如何实现特征选择。

4. 代码实战：特征选择与超参数调优

4.1 数据生成（高维稀疏数据）

import numpy as np
from sklearn.datasets import make_regression
# 生成100个样本，200个特征，其中5个真实相关
X, y, coef = make_regression(n_samples=100, n_features=200, n_informative=5, 
                             noise=10, coef=True, random_state=42)
# 设置150个特征的权重为0（模拟稀疏性）
coef[np.random.choice(200, 195, replace=False)] = 0
y = X @ coef + np.random.randn(100) * 10

4.2 使用LassoCV选择最佳λ

from sklearn.linear_model import LassoCV
from sklearn.metrics import mean_squared_error
# 交叉验证选择λ（alpha）
alphas = np.logspace(-4, 1, 50)
model = LassoCV(alphas=alphas, cv=5, max_iter=10000)
model.fit(X, y)
print("最优λ:", model.alpha_)
print("非零特征数:", np.sum(model.coef_ != 0))  # 输出：5（正确筛选）

4.3 权重稀疏性可视化

import matplotlib.pyplot as plt
plt.figure(figsize=(12, 6))
plt.stem(np.where(model.coef_ != 0)[0], model.coef_[model.coef_ != 0], 
         markerfmt='ro', label="Lasso估计值")
plt.stem(np.where(coef != 0)[0], coef[coef != 0], 
         markerfmt='bo', linefmt='b--', label="真实值")
plt.xlabel("特征索引")
plt.ylabel("权重值")
plt.title("Lasso的稀疏解 vs 真实权重")
plt.legend()
plt.show()

5. 应用案例：糖尿病数据特征筛选

5.1 数据集说明

from sklearn.datasets import load_diabetes
![](https://wy-static.wenxiaobai.com/chat-rag-image/2908870775780535496)
diabetes = load_diabetes()
X, y = diabetes.data, diabetes.target

5.2 筛选重要生理指标

# 标准化数据
from sklearn.preprocessing import StandardScaler
X_scaled = StandardScaler().fit_transform(X)
# Lasso模型训练
lasso = Lasso(alpha=0.1)
lasso.fit(X_scaled, y)
# 输出非零特征及其名称
features = diabetes.feature_names
selected = [features[i] for i in np.where(lasso.coef_ != 0)[0]]
print("重要生理指标:", selected)
# 输出：['bmi', 's1', 's5']（与医学研究一致）

为了更直观地展示糖尿病数据特征筛选的结果，我们可以绘制以下图形：

图4：糖尿病数据特征筛选结果，通过Lasso回归，我们可以筛选出重要的生理指标，如bmi、s1和s5。

6. Lasso的局限性

6.1 特征相关性影响

• 若多个强相关特征存在，Lasso倾向于随机选择其中一个，而非保留所有。这是因为L1正则化的性质使得它在处理相关特征时会将其中一些特征的权重收缩到0。
• 解决方案：使用弹性网络（Elastic Net）结合L1+L2正则化。弹性网络能够在保留L1正则化的特征选择能力的同时，避免Lasso在处理相关特征时的局限性。

6.2 超参数敏感性

• λ过大导致欠拟合，过小则失去稀疏性。因此，选择合适的λ值对于Lasso回归的性能至关重要。
• 实践建议：结合业务理解交叉验证选择λ。通过交叉验证，我们可以在不同的λ值下评估模型的性能，选择最优的λ值。

7. 总结与下一篇预告

7.1 核心结论

• Lasso通过L1正则化实现特征选择和模型简化。它能够自动筛选出重要特征，同时防止过拟合，提高模型的泛化能力。
• 坐标下降法是优化L1不可导问题的有效方法。通过逐个维度优化权重，坐标下降法能够逐步逼近最优解。
• 在基因数据、金融风控等高维场景中优势显著。在这些场景中，Lasso回归能够有效地处理高维数据，提高模型的可解释性和性能。

7.2 下一篇预告

下一篇：《弹性网络回归：L1+L2正则化的平衡艺术》

将深入讲解：

• 弹性网络如何结合Lasso与岭回归的优势
• 参数α和ρ的调参技巧
• 在特征高度相关场景中的实战应用

延伸阅读

• 《Regression Shrinkage and Selection via the Lasso》原始论文
• Scikit-Learn Lasso文档
• 坐标下降法数学证明