求组合数的四种方法

求组合数的四种方法

组合数是算法和编程中的一个常见问题，特别是在处理排列组合相关的问题时。本文将介绍四种求解组合数的方法，包括迭代法、利用乘法逆元、Lucas定理以及高精度计算。每种方法都适用于不同规模的数据范围，从基础到进阶，帮助读者全面掌握组合数的计算技巧。

组合数公式：（图来自百度百科）

1.迭代法（预处理）求组合数

适用于(C_a^b)中(a)和(b)不是很大的情况,一般(1 \leq a,b \leq 10^4)
所以可以直接预处理出来(C_a^b)，用的时候直接查表即可。
时间复杂度(O(n^2))

#include <iostream>
using namespace std;
const int N = 2010, mod = 1e9 + 7;
int c[N][N];
void init()
{
    for(int i = 0; i < N; i ++ )
        for(int j = 0; j <= i; j ++ )
            if(!j) c[i][j] = 1;
            else c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;
}
int main()
{
    init();
    int n;
    scanf("%d", &n);
    while(n --)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        printf("%d\n", c[a][b]);
    }
    return 0;
}

2.利用乘法逆元求组合数

(C_n^m = \frac{n!}{(n-m)m!})，此时(1\leq m,n \leq10^5)
对乘法逆元不熟悉的可以看这里
将组合数公式转化为除法形式：
n!
表示为
fact[n]
,
(n-m)!
表示为
infact[n - m]
，
m!
表示为
infact[m]
所以组合数公式可以写成:(C_n^m)=
fact[n] * infact[m] * infact[n - m]
infact表示逆元数组，模数是质数的情况下可以用费马小定理+快速幂求逆元
费马小定理两边同除(a)得：
所以(a)模(p)的逆元就是(a^{p-2})，这个可以用快速幂求。
时间复杂度(O(nlogn))

#include <iostream>
![](https://wy-static.wenxiaobai.com/chat-rag-image/3778030588879656276)
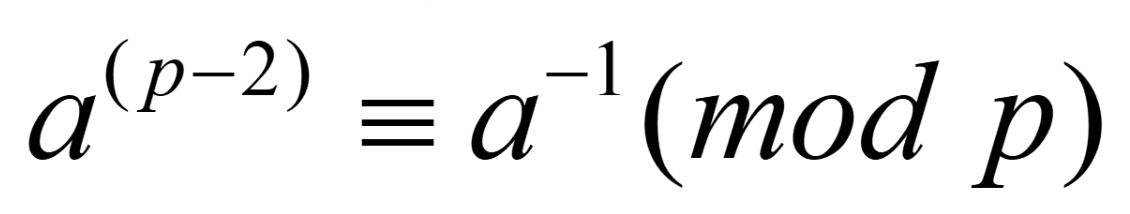
using namespace std;
typedef long long LL;
const int N = 100010, mod = 1e9 + 7;
int fact[N],infact[N];
LL qmi(LL a,int k,int p)
{
    LL res = 1;
    while(k)
    {
        if(k & 1) res = res * a % p;
        k >>= 1;
        a = a * a % p;
    }
    return res;
}
int main()
{
    //预处理阶乘和阶乘的逆元
    fact[0] = infact[0] = 1;
    for(int i = 1; i < N; i ++)
    {
        fact[i] = (LL)fact[i - 1] * i % mod;
        infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod; //这里是关键，把组合数的公式转化为乘法形式
    }
    int n;
    scanf("%d",&n);
    while(n --)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        printf("%lld\n", (LL)fact[a] * infact[a - b] % mod * infact[b] % mod);
        //因为3个1e9级别的数相乘会爆longlong，所以乘了两个后要mod一下1e9+7，不影响结果
    }
    return 0;
}

3.Lucas定理求组合数

此时(1\leq a,b \leq 10^{18})
Lucas定理：(C_a^b \equiv C_{a % p}^{b % p} \cdot C_{a / p}^{b / p} (mod \ p))
中间组合数按定义算即可：(C_a^b = \frac{a!}{(a-b)!\ b!})
时间复杂度(O(p *logn * logp))

#include <iostream>
using namespace std;
typedef long long LL;
LL qmi(LL a,int k, int p)
{
    LL res = 1;
    while(k)
    {
        if(k & 1) res = res * a % p;
        k >>= 1;
        a = a * a % p;
    }
    return res;
}
int C(int a,int b,int p)
{
    if(a < b) return 0;
    LL res = 1;
    for(int i = 1, j = a; i <= b; i ++ , j -- )
    {
        res = res * j % p;
        res = res * qmi(i, p - 2, p) % p;
    }
    return res;
}
LL lucas(LL a, LL b, int p)
{
    if(a < p && b < p) return C(a, b, p);
    return C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
int main()
{
    int n;
    cin >> n;
    while(n --)
    {
        LL a,b;
        int p;
        cin >> a >> b >> p;
        cout << lucas(a, b, p) << endl;
    }
    return 0;
}

4.高精度求组合数

这类题与其他三类题不同的地方在于，题目没有让求(C_a^b)模某个数，而是直接让你求出(C_a^b)的值
(1 \leq a,b \leq 5000)，这就需要用到高精度了。
求组合数的话还是从定义出发，(C_a^b = \frac{a!}{(a-b)!\ b!})
由算术基本定理，
同理，组合数公式中分子和分母都是用阶乘表示，阶乘当然也可以分解为有限个质数的乘积
这样我们可以把分子分母都分解质因数，然后分子和分母上的质因数还可以消掉，显然分子是一定大于分母的(组合数算下来总不能小于1吧，当然a<b的情况我们会特判掉)，所以分母中的质因子一定会被消掉，这样这个组合数公式就变成一个由若干个质因子乘积表示的式子了，所以我们只需要写一个高精度乘法就可以了。
分解质因数：
这里要求(n!)中质因子(p)出现的次数，公式如下：
质因子p的次数为：(\lfloor \frac{n}{p} \rfloor +\lfloor \frac{n}{p^2} \rfloor + \ldots+\lfloor \frac{n}{p^n} \rfloor)
上式中，第一项的含义为(1\sim n)中(p)的倍数的个数，第二项为(1\sim n)中(p^2)的倍数，依次类推...
当然，这个式子中并不一定n项都存在，大部分情况是只存在个别几项。

#include <iostream>
#include <vector>
using namespace std;
const int N = 5010;
int primes[N],cnt;
bool st[N];
int sum[N];
void get_primes(int n) //分解质因数，先用线性筛预处理出来题目范围内的所有质数
{
    for(int i = 2; i <= n; i ++ )
    {
        if(!st[i]) primes[cnt ++ ] = i;
        for(int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) break;
        }
    }
}
int get(int n, int p)//分解质因数，求n的阶乘中有多少个质因子p
{
    int res = 0;
    while(n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}
vector<int> mul(vector<int> a, int b)
{
    vector<int> c;
    int t = 0;
    for(int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    while(t)
    {
        c.push_back(t % 10);
        t /= 10;
    }
    return c;
}
int main()
{
    int a,b;
    cin >> a >> b;
    get_primes(a);
    for(int i = 0; i < cnt; i ++ )
    {
        int p = primes[i];
        sum[i] = get(a, p) - get(a - b, p) - get(b, p);
    }
    vector<int> res;
    res.push_back(1);
    for(int i = 0; i < cnt; i ++ )
        for(int j = 0; j < sum[i]; j ++ )
            res = mul(res, primes[i]);
    for(int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
    puts("");
    return 0;
}

阶乘分解

另外再补充一道阶乘分解，也需要用到分解质因数

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 1e6 + 10;
int primes[N], cnt;
bool st[N];
void init(int n)
{
    for(int i = 2; i <= n; i ++ )
    {
        if(!st[i]) primes[cnt ++ ] = i;
        for(int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) break;
        }
    }
}
int main()
{
    int n;
    scanf("%d", &n);
    init(n);
    for(int i = 0; i < cnt; i ++ )
    {
        int p = primes[i];
        int s = 0;
        for(int j = n; j; j /= p) s += j / p; //s就是每个质数的指数幂
        printf("%d %d\n", p, s);
    }
    return 0;
}