MATLAB拟合工具箱(cftool)使用教程:从基础操作到模型预测
MATLAB拟合工具箱(cftool)使用教程:从基础操作到模型预测
本文是一篇关于MATLAB拟合工具箱(cftool)使用教程的技术文章,详细介绍了如何使用该工具箱进行数据拟合、参数调整、图像导出以及模型预测等操作。文章内容结构清晰,从基础的工具箱打开方法到高级的模型预测应用,逐步深入,适合不同层次的读者学习。
一、打开matlab拟合工具箱
方法1:直接输入“cftool”
方法2:选择“apps”"curve fitting"
拟合工具箱:
二、拟合工具箱的使用
数据:
x 4.2 5.9 2.7 3.8 3.8 5.6 6.9 3.5 3.6 2.9 4.2 6.1 5.5 6.6 2.9 3.3 5.9 6 5.6
y 8.4 11.7 4.2 6.1 7.9 10.2 13.2 6.6 6 4.6 8.4 12 10.3 13.3 4.6 6.7 10.8 11.5 9.9
(1)导入数据:load data1.mat
(2) 选择合适的函数进行拟合。
参数解释:
Linear model Poly1:
f(x) = p1*x + p2
Coefficients (with 95% confidence bounds):
p1 = 2.095 (1.886, 2.304)%表明p1有95%的可能性落在[1.886,2.304]这个区间
p2 = -1.055 (-2.072, -0.03775)
Goodness of fit:
SSE: 5.728%误差平方和
R-square: 0.9635%拟合优度
Adjusted R-square: 0.9613%调整后的拟合优度
RMSE: 0.5805%均方误差
在拟合里面,最重要的两个参数是误差平方和SSE和拟合优度R^2,拟合优度越接近于1,说明误差越小,拟合效果越好。
三、自定义拟合函数——Custom Equation(建模用的较多)
在matlab拟合工具箱中,可以自定义函数的参数和表达式,matlab会自动计算出参数的值。
当拟合函数设置成一元二次函数时,可以发现拟合优度变大了,这是不是说明该二次函数比一次函数更好呢?
实际上,二次函数和一次函数的SSE和R^2的值都相差不大。在这种情况下,尽量拟合函数越简单越好,否则很可能出现龙格现象(过拟合)。
四、多项式拟合(建模用的较多)
多项式拟合可以自定义函数的阶数。
五、如何导出拟合的高清图像
(1)选择“打印图像”
(2) 选择“导出设置”“导出”或者选择“编辑”“复制图片”
分辨率可以改成“600”,这样图像的清晰度会更高一些。
六、调用拟合工具箱自动生成的代码
第一步:选择“文件”“自动生成代码”
第二步:点击保存,保存为函数格式.m的文件
第三步:点击下面的代码执行即可。
[fitresult, gof] = createFit(x, y)
通过生成的代码,可以更改坐标轴、图像标题等信息。
七、利用拟合工具箱预测美国人口
1. 题目
下表给出了近2个世纪的美国人口统计数据(单位:百万人),请使用最下面给定的拟合函数预测后30年的美国人口。
2. 使用拟合工具箱进行拟合
导入数据,调出拟合工具箱:
year = 1790:10:2000;
population = [3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];
cftool
输入自定义的拟合函数:(需要将f(x)改为f(t))
xm/(1+((xm/3.9)-1)*exp((-r)*(t-1790)))
发现拟合函数图像有问题,提示:
Fit computation did not converge:拟合计算未收敛:
Fitting stopped because the number of iterations or function evaluations exceeded the specified maximum.拟合停止,因为迭代次数或函数求值次数超过了指定的最大值。
说明拟合参数xm和r的初始值设置有问题,这就需要我们更改拟合参数xm和r的值,我们可以一个个数去试
【结果】:
General model:
f(t) = xm/(1+((xm/3.9)-1)exp((-r)(t-1790)))
Coefficients (with 95% confidence bounds):
r = 0.02735 (0.0265, 0.0282)
xm = 342.4 (311, 373.8)
Goodness of fit:
SSE: 1225
R-square: 0.9924
Adjusted R-square: 0.992
RMSE: 7.826
在这里,由于该函数不是线性函数,所以不用拟合优度解释拟合的效果,而应该用误差平方和SSE进行解释。这里SSE=1225,说明误差还比较小。
3. 自动生成拟合的代码
和第五点的操作方法一样,自动生成代码,改变一些标题等。
自动生成的代码:
function [fitresult, gof] = createFit(year, population)
%% Fit: 'untitled fit 1'.
[xData, yData] = prepareCurveData( year, population );
% Set up fittype and options.
ft = fittype( 'xm/(1+((xm/3.9)-1)*exp((-r)*(t-1790)))', 'independent', 't', 'dependent', 'y' );
opts = fitoptions( ft );
opts.Display = 'Off';
opts.Lower = [-Inf -Inf];
opts.StartPoint = [0.757740130578333 41];
opts.Upper = [Inf Inf];
% Fit model to data.
[fitresult, gof] = fit( xData, yData, ft, opts );
% Plot fit with data.
figure( 'Name', '拟合函数图像' );
h = plot( fitresult, xData, yData );
legend( h, '样本点', '拟合曲线', 'Location', 'NorthEast' );
% Label axes
xlabel( '年份' );
ylabel( '人口数(百万人)' );
grid on
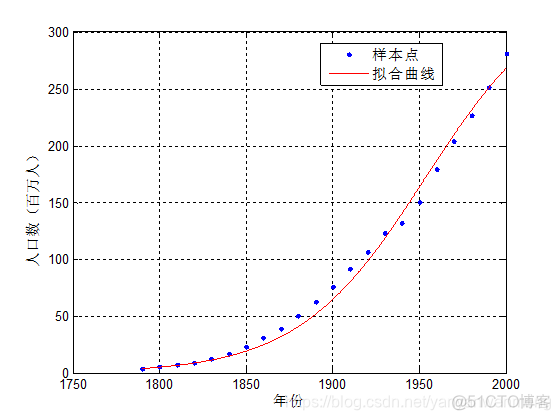
图像:
4. 预测未来的人口数
【分析】指导预测人口y=f(x)的函数关系式后,可以根据年份算出人口数。需要注意的时,计算预测的人口数时需要用点乘/除的形式,保证一个x对应一个唯一的y值,按照对应的值进行计算。
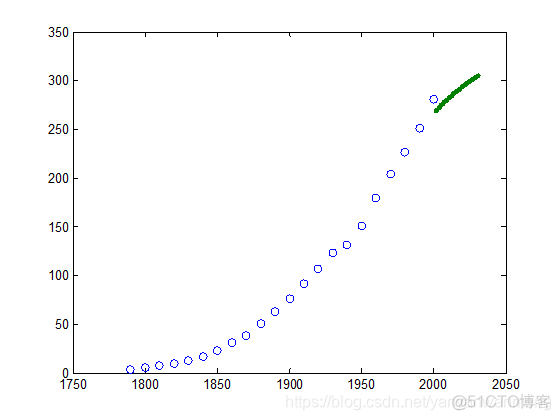
t = 2001:2030;
xm = 342.4;
r = 0.02735;
predictions = xm./(1+(xm./3.9-1).*exp(-r.*(t-1790))); % 计算预测值(注意这里要写成点乘和点除,这样可以保证按照对应元素进行计算)
计算结果:(predictions即为预测的人口数)
年份 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020 2021 2022 2023 2024 2025 2026 2027 2028 2029 2030
人口 269.4898 271.047 272.5795 274.0874 275.5707 277.0295 278.4638 279.8738 281.2595 282.621 283.9585 285.2722 286.5621 287.8285 289.0715 290.2913 291.4881 292.6621 293.8136 294.9428 296.0498 297.135 298.1986 299.2408 300.2619 301.2622 302.2419 303.2013 304.1407 305.0603
plot(year,population,'o',t,predictions,'.') % 绘制预测结果图
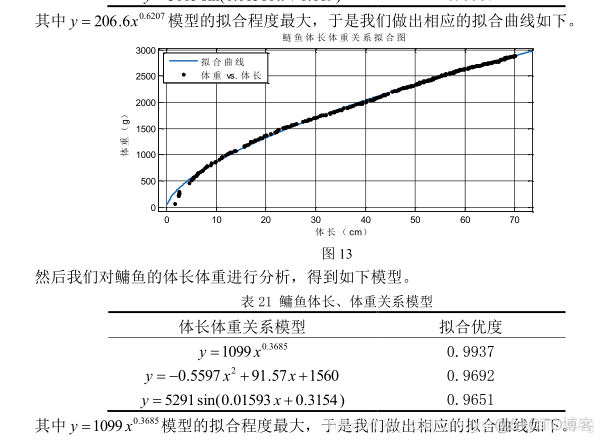
## 八、优秀论文中cftool的应用