MATLAB三维等高线图绘制详解

MATLAB三维等高线图绘制详解

引用

CSDN

1.

https://blog.csdn.net/Zachary_zzz/article/details/138697753

本文将详细介绍MATLAB中三维等高线图的绘制方法，包括基本绘制、图形美化以及动态化处理。通过本文的学习，读者将能够掌握三维等高线图的绘制技巧，更好地分析和理解三维图像的特征。

概要

本文介绍MATLAB中三维等高线图的使用方法。

整体架构流程

1. 设置三维图的参数；使用meshgrid 函数来生成网格矩阵
2. 直接调用函数contour3

基本使用----分块分析

1. 设置三维图的参数；使用meshgrid 函数来生成网格矩阵

[X,Y] = meshgrid(-5:0.25:5);
Z = X.^2 + Y.^2;

或者：

f = @(x,y) x.^2 - y.^2; %设置函数
x = linspace(-3,3, 40);% x 轴范围
y = linspace(-3,3, 40);% y 轴范围
[X,Y] = meshgrid(x, y);% 生成网格矩阵
Z = f(X,Y);

2. 直接调用函数contour3

tips：如果要分割等高线的疏密度，修改 i 处参数即可

contour3(X,Y,Z,i)

以 i = 50 为例

contour3(X,Y,Z,50)

综合·代码

f = @(x,y) x.^2 - y.^2; %设置函数
x = linspace(-3,3, 40);% x 轴范围
y = linspace(-3,3, 40);% y 轴范围
[X,Y] = meshgrid(x, y);% 生成网格矩阵
Z = f(X,Y);
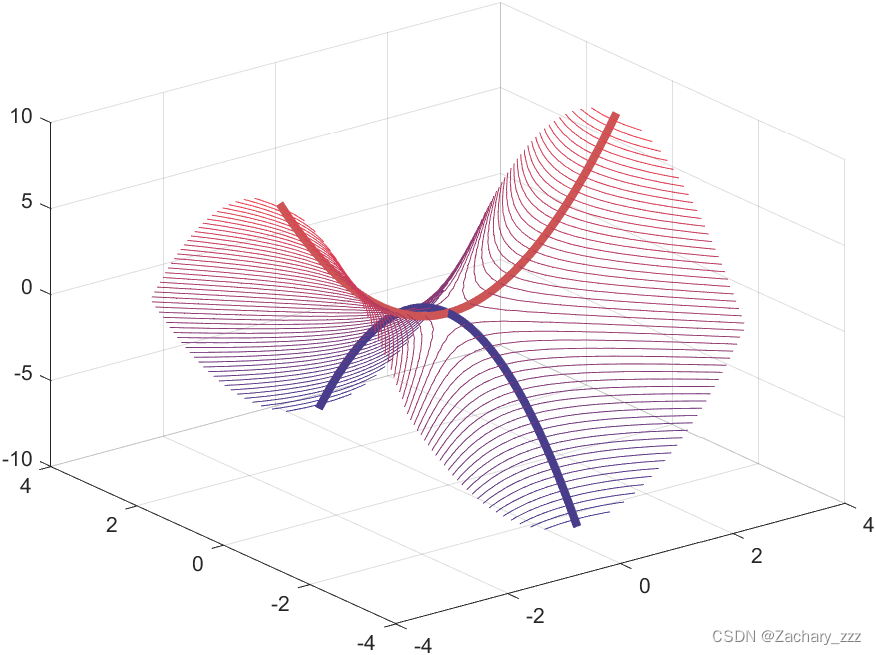
contour3(X,Y,Z,50)

代码结果展示

图形美化

其他类型详见官网
比如：

颜色修改

单色--使用十六进制

这里推荐一个非常好用的免费网站
RGB颜色表与十六进制颜色值码

contour3(X,Y,Z,50,"EdgeColor","#4682B4")

代码结果展示

渐变色--使用十六进制 + colormap
导入自己喜欢的colormap，修改等高线的颜色类型
（我这边导入的是本人自定义的colormap——red_dark ，但是MATLAB自带有一些colormap，可以使用colormap函数然后选择）

load red_dark; ... colormap(red_dark)

图形动态化

实质：修改 i 的参数

f = @(x,y) x.^2 - y.^2; %设置函数
![](https://wy-static.wenxiaobai.com/chat-rag-image/913534913122833860)
x = linspace(-3,3, 40);% x 轴范围
y = linspace(-3,3, 40);% y 轴范围
[X,Y] = meshgrid(x, y);% 生成网格矩阵
Z = f(X,Y);
for i = 10:2:50
    contour3(X,Y,Z,50,"EdgeColor","#4682B4")
    pause(0.2)% 暂停0.2秒，便于观察视图内图形的变化
end

代码结果展示

小结

我们常常因为不知道如何去把三维图形进行水平切片而感到困惑，那么使用便捷的contour3函数我们就能更加直观地去了解和分析这个三维图像的特征。