基础算法详解:枚举算法的六大类型及应用
基础算法详解:枚举算法的六大类型及应用
枚举算法是一种简单而有效的算法,它通过枚举所有可能的情况来解决问题。它通常用于解决问题规模比较小的问题,因为它的时间复杂度很高,随着问题的规模增加,算法的效率会急剧下降。
一、线性枚举
线性枚举指的是遍历某一个一维数组(顺序表)的所有元素,找到满足条件的那个元素并且返回,返回的可以是下标,也可以是元素本身。由于是遍历的,穷举了所有情况,所以一定是可以找到解的,除非问题本身无解。一些资料上也称之为暴力算法(Brute Force)
练习:
给出一个数组:int* arr[10]={3,6,2,5,8,9,7,4,1,0};要求找到7所在位置的下标是多少。
int fuc(int* arr,int n,int targ){
//arr={......};n=10;targ=7
for(int i=0;i<n;i++){
if(arr[i]==targ)return i;
}
return NULL;
}
二、二分枚举
如果在顺序表是有序的情况下,我们可以采取折半的方法去查找,这种方法称为二分枚举。
练习:
木材厂有 𝑛 根原木,现在想把这些木头切割成 𝑘k段长度均为 𝑙的小段木头(木头有可能有剩余)。当然,我们希望得到的小段木头越长越好,请求出 𝑙的最大值。木头长度的单位是 cm,原木的长度都是正整数,我们要求切割得到的小段木头的长度也是正整数。
例如有两根原木长度分别为 11和 21,要求切割成等长的 6 段,很明显能切割出来的小段木头长度最长为 5。
#include<vector>
#include<algorithm>
#include<iostream>
using namespace std;
int maxLength(vector<int> v, int k)
{
//二分的前提是顺序表有序
sort(v.begin(), v.end());
int m = v[v.size()-1];
int left = 0;
int right = m;
int mid = (right - left) / 2 + left;
while (left < right)
{
if (right-left == 1) {//如果木段差==1,就该考虑返回left还是返回right
int s = 0;
for (auto e : v) {
s += (e / right);
}
if (s >= k)return right;//如果总段数大于k说明至少能截成k个right.
return left;//没能进入返回
}
int sum = 0;//段数和
for (auto e : v) {
//每根原木的长度÷估计的最大段长->可截段数
//每根原木的可截段数 求总和
sum += (e / mid);
}
//二分
if (sum >= k) {
//根据中值求总段数,可以获得比标准数量更多的小木段
//那么可以试着大一点,更新左值
left = mid;
}
else if (sum < k) {
//根据中值不能获取足够的小木段
//那么可以试着小一点,更新右值
right = mid-1;
}
mid = (right - left) / 2 + left;//中值--更新mid
}//时间复杂度O(nlogn),此时n为最短元素大小
return mid;//结果理论为:left==mid==right
}
int main()
{
int N, K; //N原木个数,K目标段数
cin >> N >> K;
vector<int> v(N);
for (int i = 0; i < N; i++)
cin >> v[i];//每根原木长度
cout << maxLength(v, K) << endl;
return 0;
}
三、三分枚举
三分枚举是一种用于求解单峰(单谷)函数极值的算法。它的基本原理是利用函数的单峰(单谷)性质,通过迭代的方式逐步缩小搜索范围,最终找到极值点。具体来说:对于形如y=ax²+bx+c的二次函数,其极值点位于x=-b/2a。如果给定一个包含极值点的区间,可以通过三分法逐步缩小区间范围,直到找到极值点。
练习:
牛牛有x件材料a和y件材料b,用2件材料a和3件材料b可以合成一件装备,用4件材料a和1件材料b也可以合成一件装备。牛牛想要最大化合成的装备的数量,于是牛牛找来了你帮忙。
输入包含t组数据
第一行一个整数t
接下来t行每行两个整数x,y
每组数据输出一行一个整数表示答案。
假设方案一做了m件装备,方案二做了n件装备,我们遍历m来求n,n=min((x-2m)/4, y-3m),三分m,求n+m的最大值
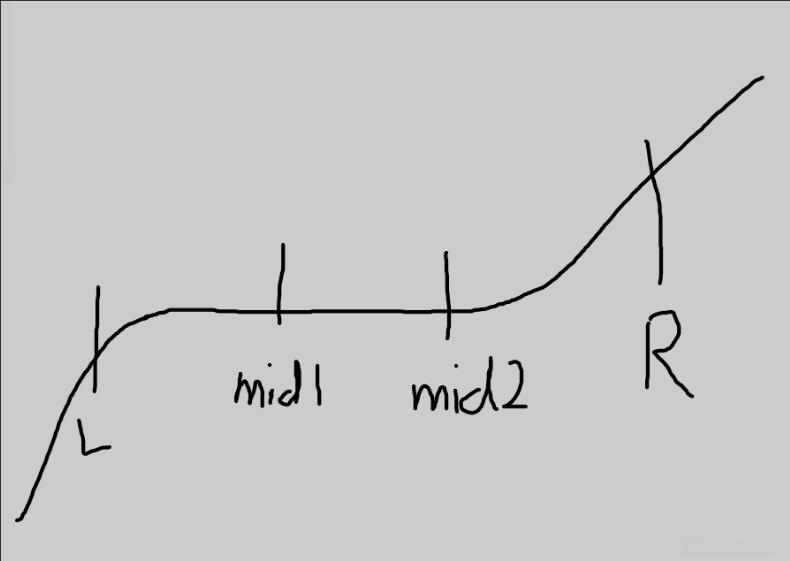
由于三分时返回的m+n是整数,注意下面的情况时check(mid1)==check(mid2)&&check(mid1)<check(R) ,L=mid1+1,而不是R=mid2-1
#include <bits/stdc++.h>
using namespace std;
int x, y;
int check(int m){
return m+min((x-2*m)/4, y-3*m);
}
int main(){
int T;
cin>>T;
while(T--){
cin>>x>>y;
int L=0, R = min(x/2, y/3);
int ans = 0;
while(L<=R)
{
int mid1 = L+(R-L)/3, mid2 = R-(R-L)/3;
int res1 = check(mid1), res2 = check(mid2);
ans = max(res1, res2);
if(res1<res2||(res1==res2&&res1<check(R))) L = mid1+1;
else R = mid2-1;
}
cout<<ans;
}
return 0;
}
四、暴力枚举
暴力枚举,顾名思义,就是将问题的所有可能解逐一列举出来,然后一一验证,直到找到正确解。这种方法虽然看似粗暴,但对于规模较小的问题或者没有更优解法的情况下,往往是最直接有效的方法。数组的线性枚举就是暴力枚举的一种。
练习:
X星系的机器人可以自动复制自己。它们用1年的时间可以复制出2个自己,然后就失去复制能力。
每年X星系都会选出1个新出生的机器人发往太空。也就是说,如果X星系原有机器人5个,
1年后总数是:5 + 9 = 14
2年后总数是:5 + 9 + 17 = 31
如果已经探测经过n年后的机器人总数s,你能算出最初有多少机器人吗?
输入:输入一行两个数字n和s,用空格分开,含义如上。n不大于100,s位数不超过50位。
输出:要求输出一行,一个整数,表示最初有机器人多少个。
从有一个开始试,试到n年,看此时的结果是不是输入的总人数。是就输出并退出,不是的话就继续。今年能产生的机器人数量=去年的*2-1。然后把今年产生的加在总count里。判断count和输入的一不一样。
#include <iostream>
using namespace std;
#define Long long long
int main() {
int n;
Long total,count = 0;
Long thisYear=0,lastYear=0 ;
cin >> n >>total;
for (int i = 1; i < total; ++i) {
count = thisYear = i;
for (int j = 0; j < n; ++j) {
lastYear = thisYear;
thisYear = lastYear*2-1;
count += thisYear;
}
if (count == total) {
cout << i;
return 0;
}
//else continue;
}
}
五、排列组合枚举
简介:
- 排列枚举:给定 n 个元素,枚举其所有的 r 元素排列可以使用递归或回溯的方法。
- 组合枚举:同样地,组合的枚举也可以使用递归的方式来实现。
递归传送门:基础算法--递归算法【难点、重点】-CSDN博客
练习:
生成给定数组的所有排列组合:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
void permute(vector<int>& nums, int start) {
if (start == nums.size() - 1) {
// 输出当前排列
for (int num : nums) {
cout << num << " ";
}
cout << endl;
}
else {
for (int i = start; i < nums.size(); ++i) {
swap(nums[start], nums[i]); // 交换
permute(nums, start + 1); // 递归
swap(nums[start], nums[i]); // 撤销交换
}
}
}
void combine(const vector<int>& nums, int r, int start, vector<int>& path) {
if (path.size() == r) {
// 输出当前组合
for (int num : path) {
cout << num << " ";
}
cout << endl;
return;
}
for (int i = start; i < nums.size(); ++i) {
path.push_back(nums[i]); // 添加当前元素
combine(nums, r, i + 1, path); // 递归
path.pop_back(); // 撤销添加
}
}
int main() {
vector<int> vec = {1, 2, 3};
permute(vec, 0);
vector<int> nums = {1, 2, 3};
int r = 2; // 组合的大小
vector<int> path;
combine(nums, r, 0, path);
return 0;
}
- 排列枚举: 这个程序通过交换当前元素和其他元素的位置,然后递归处理下一个位置,最终列出所有可能的排列。
- 组合枚举: 这个程序通过递归构建组合,每次选择当前元素并继续下一次迭代。通过path存储当前组合,达到组合大小后输出结果。
六、状压DP
状压DP是一种用于解决状态压缩动态规划问题的算法。它通常用于处理具有大量状态但状态之间存在某种规律性的问题。通过将状态压缩成二进制数,可以有效地减少状态空间,从而降低算法的时间复杂度。状压DP在解决某些组合优化问题时非常有效,例如旅行商问题、子集和问题等。
练习:
给出一个长度为n的数组,每个元素的值为0或1。你需要找到一个最长的子序列,使得该子序列中0和1的数量相等。输出这个最长子序列的长度。
#include <iostream>
#include <vector>
using namespace std;
int longestBalancedSubsequence(vector<int>& nums) {
int n = nums.size();
vector<int> dp(1 << n, 0);
int maxLen = 0;
for (int mask = 1; mask < (1 << n); ++mask) {
int zeros = 0, ones = 0;
for (int i = 0; i < n; ++i) {
if (mask & (1 << i)) {
if (nums[i] == 0) {
zeros++;
} else {
ones++;
}
}
}
if (zeros == ones) {
dp[mask] = 2 * zeros;
maxLen = max(maxLen, dp[mask]);
} else {
for (int i = 0; i < n; ++i) {
if (mask & (1 << i)) {
dp[mask] = max(dp[mask], dp[mask ^ (1 << i)]);
}
}
}
}
return maxLen;
}
int main() {
vector<int> nums = {0, 1, 0, 1, 0, 1};
cout << longestBalancedSubsequence(nums) << endl;
return 0;
}
在这个例子中,我们使用了一个大小为2^n的dp数组来存储所有可能的状态。对于每个状态mask,我们计算其中0和1的数量。如果0和1的数量相等,我们就更新dp[mask]为2倍的这个数量,并更新maxLen。否则,我们尝试从mask中移除一个元素,看看是否能得到一个更长的平衡子序列。
这种方法的时间复杂度为O(n * 2^n),空间复杂度为O(2^n)。虽然时间复杂度较高,但对于n较小的情况(例如n <= 20)仍然可以接受。