温故知新，数学之美，以毕达哥拉斯为线索，告诉你数学从猜想到定理再到应用的全过程

创作时间:

作者:

@小白创作中心

温故知新，数学之美，以毕达哥拉斯为线索，告诉你数学从猜想到定理再到应用的全过程

引用

来源

https://www.cnblogs.com/taylorshi/p/18468692

勾股定理是几何学中一个基本且重要的定理，主要应用于直角三角形。该定理描述了直角三角形三个边之间的关系：在一个直角三角形中，直角两边的平方和等于斜边的平方。

[a^2 + b^2 = c^2 ]

勾股定理在中国和世界历史上都有悠久的发展历程。在中国，据汉朝的数学书《周髀算经》记载，早在公元前1000年的时候，周公和商高就谈到了“勾三股四弦五”。而在世界范围内，从巴比伦泥板到埃及的《莱因德数学纸草书》，再到古印度的《俾舍数学》，都有关于勾股定理的记载。最终，古希腊数学家毕达哥拉斯系统化了这一定理，并给出了严格的证明。

数学定理确立的过程

在自然科学中，一个假说通过实验证实，就变成了定律。但在数学上，用实验来验证一个假说（在数学上常常被称为猜想）是不被允许的。数学的结论只能从逻辑出发，通过归纳或者演绎得出来。它必须完全正确，没有例外，因为但凡有一个例外（也被称为反例），就要被完全否定掉。

以勾股定理为例，它的确立，其实教会了人们在平面计算距离的方法，在此基础之上，三角学才得以建立，笛卡尔的解析几何才得以确立，再往上才能建立起微积分等数学工具。如果出现了一个违反毕达哥拉斯定理的反例，不仅是这个定理失效了，而且整个数学就完蛋了，我们的科技也就时灵时不灵了。因此，数学上的每一个定理，必须也只能通过逻辑推演来证明，用多少实例来验证都没有用。

应用示例-计算两点之间直线距离

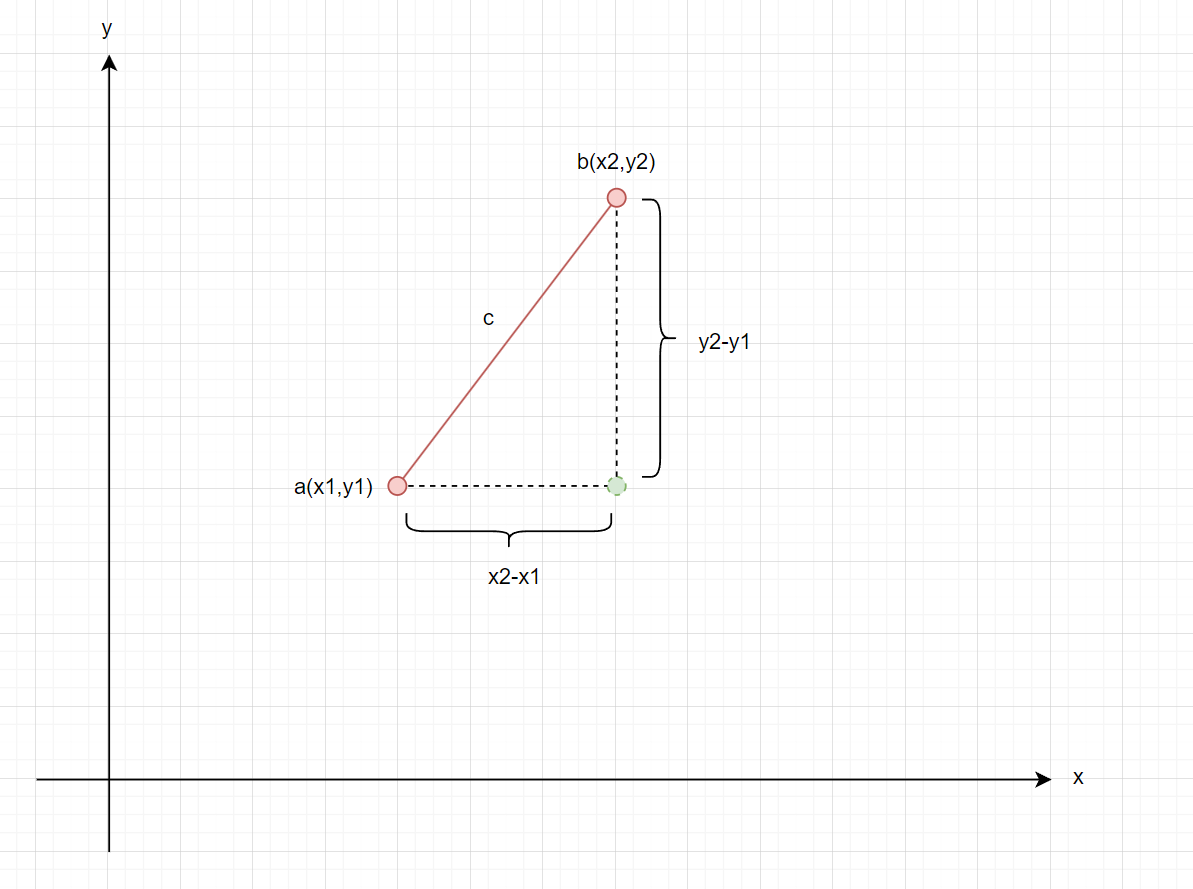
当在同一个坐标系里，已知点a的坐标是x1, x2; 已知点b的坐标是x2, y2; 那么我们怎么才能知道点a和点b之间的直线距离是多少呢？

如上图所示，当我们把点a和点b都放在同一坐标系中时，沿坐标轴x、y分别做虚线，会相交得到一个直角，此时，我们需要知道的两点之间直线距离就是，这条斜边c，这样一个关系刚好就构成了一个勾股定理的几何模型。

此时的，勾等于x2- x1，股等于y2- y1，那么两点之间的距离就是弦的数值。

internal class Program
{
![](https://wy-static.wenxiaobai.com/chat-rag-image/13893783890847302305)
    static void Main(string[] args)
    {
        Console.WriteLine("两点直线距离计算器");
        // 输入第一个点a的x坐标
        Console.Write("请输入第一个点a的x坐标数值(x1)：");
        double x1 = ReadPositiveDouble();
        // 输入第一个点a的y坐标
        Console.Write("请输入第一个点a的y坐标数值(y1)：");
        double y1 = ReadPositiveDouble();
        // 输入第二个点b的x坐标
        Console.Write("请输入第二个点b的x坐标数值(x2)：");
        double x2 = ReadPositiveDouble();
        // 输入第二个点b的y坐标
        Console.Write("请输入第二个点b的y坐标数值(y2)：");
        double y2 = ReadPositiveDouble();
        var x = Math.Abs(x2 - x1);
        Console.WriteLine($"x2 - x1的数值(x)：{x:F2}");
        var y = Math.Abs(y2 - y1);
        Console.WriteLine($"y2 - y1的数值(y)：{y:F2}");
        // 计算斜边
        double c = Math.Sqrt(x.Square() + y.Square());
        Console.WriteLine($"\n根据勾股定理，两点直线距离（c）为：{c:F2}");
    }
    /// <summary>
    /// 读取用户输入的双精度整数并进行验证
    /// </summary>
    /// <returns>有效的双精度整数</returns>
    static double ReadPositiveDouble()
    {
        double value;
        while (true)
        {
            string input = Console.ReadLine();
            if (double.TryParse(input, out value))
            {
                return value;
            }
        }
    }
}

另外，如果是三维空间的话，还需要考虑z轴上的差异。