【算法笔记】树形DP算法总结&详解
【算法笔记】树形DP算法总结&详解
0. 定义
树形DP,又称树状DP,即在树上进行的DP,是DP(动态规划)算法中较为复杂的一种。
1. 基础
令(f[u]=~)与树上顶点(u)有关的某些数据,并按照拓扑序(从叶子节点向上到根节点的顺序)进行(\text{DP}),确保在更新一个顶点时其子节点的dp值已经被更新好,以更新当前节点的(\text{DP})值。为方便计算,一般写成dfs的形式,如下:
void dfs(int v) { // 遍历节点v
dp[v] = ...; // 初始化
for(int u: G[v]) { // 遍历v的所有子节点
dfs(u);
update(u, v); // 用子节点的dp值对当前节点的dp值进行更新
}
}
下面来看一道简单的例题:
【例1.1】子树大小
给定一棵有(N)个结点的树,根结点为结点(1)。对于(i=1,2,\dots,N),求以结点(i)为根的子树大小(即子树上结点的个数,包括根结点)。
本题明显可以使用树形DP的方法,令(f[v]=~)以(v)为根的子树大小,则易得
[f[v]=1+\sum_{i=1}^{\text{deg}_v} G[v][i] ]
即:一个结点的子树大小(=1)(根节点)(+)每个子树的大小。
沿用刚才的模板,可得:
#include <cstdio>
#include <vector>
#define maxn 100
using namespace std;
vector<int> G[maxn]; // 邻接表
int sz[maxn]; // dp数组,sz[v] = 子树v的大小
void dfs(int v)
{
sz[v] = 1; // 初始化,最初大小为1,后面累加
for(int u: G[v]) // 遍历子结点
{
dfs(u); // 先对子结点进行dfs
sz[v] += sz[u]; // 更新当前子树的大小
}
}
int main()
{
int n;
scanf("%d", &n); // 结点个数
for(int i=1; i<n; i++) // N-1条边
{
int u, v;
scanf("%d%d", &u, &v); // 读入一条边
G[u].push_back(v); // 存入邻接表
}
dfs(1);
for(int i=1; i<=n; i++)
printf("%d\n", sz[i]);
return 0;
}
下面来看一道稍微复杂一点的题:
【例1.2】洛谷P1352没有上司的舞会
本题即树的最大独立集问题。
有(N)名职员,编号为(1\dots N),他们的关系就像一棵以老板为根的树,父节点就是子节点的直接上司。每个职员有一个快乐指数(r_i),现在要召开一场舞会,使得没有职员和直接上司一起参会。主办方希望邀请一部分职员参会,使得所有参会职员的快乐指数总和最大,求这个最大值。
令(f(v))表示以(v)为根的子树中,选择(v)的最优解,(g(v))表示以(v)为根的子树中,不选(v)的最优解。
则对于每个状态,都存在两种决策(其中(u)代表(v)的儿子):
- 不选(v)时,可选也可不选(u),此时有(g(v)=\sum\max{f(u),g(u)});
- 选择(v)时,一定不能选(u),此时有(f(v)=r_i+\sum g(u))。
时间复杂度为(\mathcal O(N))。
注意本题需要寻找根节点,没有上司的结点即为根节点,读入时用数组标记即可。
#include <cstdio>
#include <vector>
#define maxn 6005
using namespace std;
inline int max(int x, int y) { return x > y? x: y; }
vector<int> G[maxn]; // 邻接表
bool bad[maxn]; // 根结点标记
int f[maxn], g[maxn]; // 数据存储
void dfs(int v) // 遍历结点v
{
// 读入时已初始化,这里可省略
for(int u: G[v]) // 遍历子结点
{
dfs(u); // 先对子结点进行dfs
// 更新当前dp状态
f[v] += g[u]; // 选择v,不能选u
g[v] += max(f[u], g[u]); // 不选v,u可选可不选
}
}
int main()
{
int n;
scanf("%d", &n); // 结点个数
for(int i=0; i<n; i++)
scanf("%d", f + i); // 相当于提前初始化好f[i]=r[i]
for(int i=1; i<n; i++) // N-1条边
{
int u, v;
scanf("%d%d", &u, &v); // 读入一条边
G[--v].push_back(--u); // 0-index,存入邻接表
bad[u] = true; // 标记不可能是根结点
}
int root = -1; // 根结点变量
for(int i=0; i<n; i++)
if(!bad[i]) // 找到根结点
{
root = i; // 记录根结点
break;
}
dfs(root); // 开始进行树形DP
printf("%d\n", max(f[root], g[root])); // 根结点也有两种选择
return 0;
}
习题
- HDU 2196 Computer/vjudge链接
- POJ 1463 Strategic game
- 洛谷 P3574 [POI2014] FAR-FarmCraft
2. 树上背包
在基本算法之上,树形dp还可以用于树上背包问题。来看一道例题:
【例2.1】洛谷P2014/AcWing 286选课
有(N)门课,第(i)门课的学分是(s_i)。每门课有不超过一门先修课,需要上了先修课才能上这门课。现要选(M)门课,使得学分总和最大。
每门课最多只有一门先修课,这符合树结构的特点,与有根树中一个点最多只有一个父亲结点的特点类似。因此,我们根据数据构造一棵树,课程的先修课为这门课的父结点。又由于给定的输入是一个森林(多棵树组成的不一定连通的图),不是一棵完整的树,因此我们添加虚拟根结点(0)((s_0=0)),将没有先修课的结点全部连到它下面,并从这里开始dfs。注意此时必须选中(0)号结点(它是所有课程的直接或间接先修课),所以操作前先将(M)加上(1)。
格式问题解决,下面考虑如何(\text{DP})。
令(f[i][j])表示当前在结点(i)、且已经选了(j)门课时的最大学分数量,则答案为(f[0][M+1])。状态转移方程等详见代码。时间复杂度为(\mathcal O(NM)),有兴趣的可以自己尝试证明。
#include <cstdio>
#include <vector>
#include <algorithm>
#define maxn 305
using namespace std;
// dp算法中常用的模板,等效于x=max(x,y)
inline void setmax(int& x, int y)
{
if(x < y) x = y;
}
vector<int> G[maxn]; // 邻接表
int n, m, f[maxn][maxn];
int dfs(int u) // 遍历结点u,返回值为其子树大小
{
int tot = 1; // 记录子树大小,初始为1
for(int v: G[u]) // 遍历u的所有子结点
{
int sz = dfs(v); // 对当前子结点进行搜索
// 状态转移,注意i倒序,防止串连转移现象
for(int i=min(tot, m); i>0; i--) // 子树大小优化可降低算法复杂度
for(int j=1, lim=min(sz, m-i); j<=lim; j++)
setmax(f[u][i + j], f[u][i] + f[v][j]); // 更新状态
tot += sz; // 加到当前子树下
}
return tot; // 返回子树大小
}
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++)
{
int a;
scanf("%d%d", &a, f[i] + 1); // 初始化f[i][1]=s[i]
G[a].push_back(i);
}
m ++; // 别忘了这一句
dfs(0);
printf("%d\n", f[0][m]);
return 0;
}
习题
- LOJ #2546. 「JSOI2018」潜入行动
- LOJ #2268. 「SDOI2017」苹果树
3. 换根 DP
换根DP,即为不知道根结点时使用的一种树形DP,时间复杂度一般为(\mathcal O(N))。
【例3.1】洛谷 P3478[POI2008] STA-Station
给定一个(n)个点的树,请求出一个结点,使得以这个结点为根时,所有结点的深度之和最大。
先考虑最简单粗暴的方法,即为枚举所有结点,代码如下:
#include <cstdio>
#include <vector>
#define maxn 1000005
using namespace std;
vector<int> G[maxn];
int dfs(int v, int d, int par)
{
int s = d;
for(int u: G[v])
if(u != par)
s += dfs(u, d + 1, v);
return s;
}
int main()
{
int n;
scanf("%d", &n);
for(int t=n; --t; )
{
int u, v;
scanf("%d%d", &u, &v);
G[--u].push_back(--v);
G[v].push_back(u);
}
int ans = 0, maxDepth = dfs(0, 0, -1);
for(int root=1; root<n; root++)
{
int d = dfs(root, 0, -1);
if(d > maxDepth) ans = root, maxDepth = d;
}
printf("%d\n", ++ans);
return 0;
}
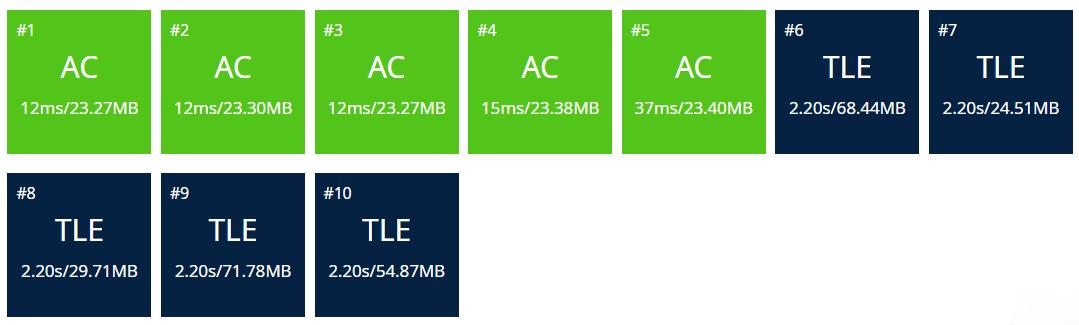
很明显,这种做法时间复杂度为(\mathcal O(n^2)),又因为(n\le 10^6),所以无法得全分,评测结果如下:
好家伙,居然还有50分,本以为最多30..
下面来考虑换根DP的方法。不妨令(u)为当前结点,(v)为其子结点。先预处理出每个结点的子树大小(s[u]=1+\sum s[v])和以(1)为根结点时所有结点的深度((\text{depth}_i)),此时第一遍DFS即为预处理。
令(f_u)表示以(u)为根时,所有结点的总深度和,则(f_1=\sum\text{depth}_i)。
考虑(f_u\to f_v)的转移,即“根结点从(u)变成(v)时所有结点深度和的变化”,则有:
- 所有在(v)的子树上的结点深度全部(-1),则总深度和减少(s_v);
- 所有不在(v)的子树上的结点深度都(+1),则总深度和增加(n-s_v);
此时,可得(f_v=f_u-s_v+n-s_v=f_u+n-2s_v)。注意数据类型,使用
long long
。
#include <cstdio>
#include <vector>
#define maxn 1000005
using namespace std;
using LL = long long;
vector<int> G[maxn];
LL sz[maxn], f[maxn];
int n, ans;
LL dfs1(int v, int d, int par)
{
sz[v] = 1;
LL s = d;
for(int u: G[v])
if(u != par)
s += dfs1(u, d + 1, v), sz[v] += sz[u];
return s;
}
void dfs2(int v, int par)
{
if(f[v] > f[ans]) ans = v;
for(int u: G[v])
if(u != par)
{
f[u] = f[v] + n - (sz[u] << 1LL);
dfs2(u, v);
}
}
int main()
{
scanf("%d", &n);
for(int t=n; --t; )
{
int u, v;
scanf("%d%d", &u, &v);
G[--u].push_back(--v);
G[v].push_back(u);
}
f[0] = dfs1(0, 0, -1);
dfs2(0, -1);
printf("%d\n", ++ans);
return 0;
}
习题
- POJ 3585 Accumulation Degree
- 洛谷 P2986 [USACO10MAR] Great Cow Gathering G
- CodeForce 708C Centroids
- ABC 222F - Expensive Expense
4. 后记
好像这玩意也并不是开头所说的那么难…… 记得给个三连哦!
参考文献:
- 树形 DP - OI wiki
- 树形dp - tom0727's blog
- 【动态规划】树形DP完全详解! - RioTian - 博客园