分治法详解：从汉诺塔到快速排序

分治法详解：从汉诺塔到快速排序

引用

CSDN

1.

https://m.blog.csdn.net/2302_82116250/article/details/144411572

分治法是一种重要的算法设计策略，广泛应用于各种计算机科学问题中。本文将详细介绍分治法的基本概念、应用场景以及具体实现方法，通过汉诺塔、归并排序和快速排序等经典案例，帮助读者深入理解分治法的思想和应用。

一、分治法简介

1. 分治法概念

分治法的基本思想是将一个复杂的问题分解成若干个规模较小的子问题，然后递归地解决这些子问题，最后将子问题的解合并成原问题的解。具体操作是把原问题分为k个规模较小的子问题，对k个子问题分别求解，如果子问题的规模仍然不够小，则再划分为k个子问题。如此递归地进行下去，直到问题规模足够小，很容易求出其解为止。

分治法的思想，几乎就是递归的过程。

2. 应用场景

• 平衡子问题：子问题的规模大致相同。
• 独立子问题：子问题之间相互独立。

3. 解题步骤

1. 分解：把问题分解成独立的子问题
2. 解决：解决递归子问题
3. 合并：把子问题的结果合并成原问题的解

二、具体应用

1. 汉诺塔

问题描述

有三根柱子 A、B 和 C，以及一堆大小不同的盘子，这些盘子最初都叠放在柱子 A 上，按照从大到小的顺序。任务是将这堆盘子移动到柱子 C 上，同时保持每根柱子上的盘子顺序不变，即大盘子始终在小盘子下面。

解决思路

1. 将 n-1 个盘子从柱子 A 借助柱子 C 移动到柱子 B
2. 将最大的盘子（第 n 个盘子）从柱子 A 移动到柱子 C
3. 将 n-1 个盘子从柱子 B 借助柱子 A 移动到柱子 C

#include <iostream>
using namespace std;
int sum = 0, m;

// 递归函数来解决汉诺塔问题
void hanoi(int n, char source, char target, char auxiliary) {
    if (n == 1) {
        sum++;
        if (sum == m)
            cout << "Move disk 1 from " << source << " to " << target << endl;
    } else {
        hanoi(n - 1, source, auxiliary, target);
        sum++;
        if (sum == m)
            cout << "Move disk " << n << " from " << source << " to " << target << endl;
        hanoi(n - 1, auxiliary, target, source);
    }
}

int main() {
    int n;
    cin >> n >> m;
    hanoi(n, 'A', 'C', 'B');
    cout << sum << endl;
    return 0;
}

2. 归并排序

具体思路

1. 分解：把原来无序的数列分为两部分，对每部分继续分成更小的两部分（在归并排序中，只是把序列分为简单的两部分；在快速排序中，是把序列分成左右两部分，左部分的元素都小于右半部分的元素）
2. 解决：分解直到不能分为止，排序
3. 合并：把每次分开的两部分合并到一起

int *b = (int *)malloc(n * sizeof(int));   // 辅助数组

void merge(int a[], int left, int mid, int right) {
    int i, j, k;
    for (k = left; k <= right; ++k) {
        b[k] = a[k];  // 复制a到b
    }
    // 合并
    for (i = left, j = mid + 1, k = i; i <= mid && j <= right; k++) {
        if (b[i] <= b[j]) {    // 如果左指针的值小于右指针的值
            a[k] = b[i];      // 放入左指针的值
            i++;
        } else {
            a[k] = b[j];
            j++;
        }
    }
    // 合并左平区剩余的元素
    while (i <= mid) {
        a[k++] = b[i++];
    }
    // 合并右平区剩余的元素
    while (j <= right) {
        a[k++] = b[j++];
    }
    // 把临时数组中合并后的元素复制回原来的数组
    while (left <= right) {
        b[left] = a[left];
        left++;
    }
}

void mergeSort(int a[], int left, int right) {
    if (left < right) {
        int mid = (left + right) / 2;
        mergeSort(a, left, mid);  // 递归划分左半部分
        mergeSort(a, mid + 1, right);  // 递归划分右半部分
        merge(a, left, mid, right);   // 合并已经排序的部分
    }
}

3. 快速排序

思路

把序列分为左右两部分，使左边所有数都比右边的数小；递归这个过程，直到不能再分为止。

具体操作

递归地选择一个枢纽元素pivot，不断对当前序列进行划分，使当前序列左边元素都不超过该pivot，右边都大于该pivot。

pivot选择的方式

1. 选择序列的第一个元素、最后一个元素或者中间元素作为基准元素（缺点：当序列已经接近有序，则会导致快速排序的性能下降。快速排序的最坏情况发生在每次选择的基准元素是当前数组中的最大或最小元素）
2. 选择序列的中位数作为基准值（可以保证基准值不是当前划分序列的最大或者最小元素）
3. 随机选择一个元素作为基准值（对任意输入数据的平均算法复杂度都能达到O(nlogn)）

举例

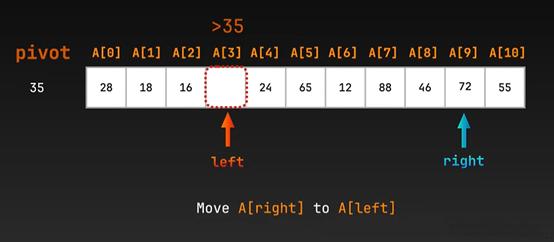
假设存在数组A = [35，18，16，72，24，65，12，88，46，28，55]

首先将首元素存到变量 pivot中，同时令left、right同时指向数组的首位元素

当A[ right ] > 35，就把right不断左移（right --）,直到A[ right ] <= pivot，就交换 left 和 right 的值

接着移动 left 指针 ，A[ left ] <= 35，就把left不断右移（left++）,直到A[ left ] >= pivot，交换left和right

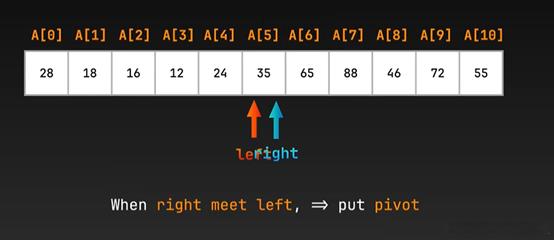
不断重复上述过程，直到 left=right ，将pivot放入相遇处

再先后对左半部分和右半部分进行上述相同的操作，不断重复直至排序结束

// 对区间[left, right]进行划分
![](https://wy-static.wenxiaobai.com/chat-rag-image/3565225096223695191)
int partition(int A[], int left, int right) {
![](https://wy-static.wenxiaobai.com/chat-rag-image/15790016961501062004)
    int pivot = A[left]; // 选择当前区间首元素作为pivot
![](https://wy-static.wenxiaobai.com/chat-rag-image/11375466467636950026)
    while (left < right) {
![](https://wy-static.wenxiaobai.com/chat-rag-image/217432010895567642)
        while (left < right && A[right] > pivot) right--; // 反复左移right
        A[left] = A[right]; // 将A[right]挪到A[left]处
        while (left < right && A[left] <= pivot) left++; // 反复右移left
        A[right] = A[left]; // 将A[left]挪到A[right]处
    }
    A[left] = pivot; // 把pivot放到left与right相遇的地方
    return left; // 返回相遇时的序列下标
}

// left与right初值为序列首尾下标（例如0和n-1，n为序列元素个数）
void quickSort(int A[], int left, int right) {
    if (left < right) { // 当前区间的长度超过1
        // 根据当前序列的pivot将[left, right]一分为二
        int pos = partition(A, left, right);
        quickSort(A, left, pos - 1); // 对左子区间递归进行快速排序
        quickSort(A, pos + 1, right); // 对右子区间递归进行快速排序
    }
}

补充第二、三种取pivot方式的实现快速排序的代码

int find3MedianIndex(int A[], int first, int middle, int last) {
    return (A[first] > A[middle]) ?
        ((A[middle] > A[last]) ? middle : ((A[first] > A[last]) ? last : first));
        ((A[first] > A[last]) ? first : ((A[middle] > A[last]) ? last : middle));
}

// 对区间[left, right]进行划分
int partition(int A[], int left, int right) {
    // 选择当前区间首元素、元素的中位数以及尾元素的中位数为pivot
    int pivotIndex = find3MedianIndex(A, left, (left + right) / 2, right);
    swap(A, left, pivotIndex); // 将得到的中位数和首元素交换 => 固定位置法
    int pivot = A[left]; // 选择当前区间首元素作为pivot
    while (left < right) {
        while (left < right && A[right] > pivot) right--; // 反复左移right
        A[left] = A[right]; // 将A[right]挪到A[left]处
        while (left < right && A[left] <= pivot) left++; // 反复右移left
        A[right] = A[left]; // 将A[left]挪到A[right]处
    }
    A[left] = pivot; // 把pivot放到left与right相遇的地方
    return left; // 返回相遇时的序列下标
}

// left与right初值为序列首尾下标（例如0和n-1，n为序列元素个数）
void quickSort(int A[], int left, int right) {
    if (left < right) { // 当前区间的长度超过1
        // 根据当前序列的pivot将[left, right]一分为二
        int pos = partition(A, left, right);
        quickSort(A, left, pos - 1); // 对左子区间递归进行快速排序
        quickSort(A, pos + 1, right); // 对右子区间递归进行快速排序
    }
}

// 对区间[left, right]进行划分
int randPartition(int A[], int left, int right) {
    // 生成[left, right]内的随机数
    int pivotIndex = (int)(1.0 * rand() / RAND_MAX * (right - left) + left);
    swap(A, left, pivotIndex); // 将得到的中位数和首元素交换 => 固定位置法
    int pivot = A[left];
    while (left < right) {
        while (left < right && A[right] > pivot) right--; // 反复左移right
        A[left] = A[right]; // 将A[right]挪到A[left]处
        while (left < right && A[left] <= pivot) left++; // 反复右移left
        A[right] = A[left]; // 将A[left]挪到A[right]处
    }
    A[left] = pivot; // 把pivot放到left与right相遇的地方
    return left; // 返回相遇时的序列下标
}

void quickSort(int A[], int left, int right) {
    if (left < right) { // 当前区间的长度超过1
        // 根据当前序列的pivot将[left, right]一分为二
        int pos = partition(A, left, right);
        quickSort(A, left, pos - 1); // 对左子区间递归进行快速排序
        quickSort(A, pos + 1, right); // 对右子区间递归进行快速排序
    }
}

本文原文来自CSDN