主成分分析法求数据前n个主成分

主成分分析法求数据前n个主成分

引用

CSDN

1.

https://m.blog.csdn.net/sujiangming/article/details/146242716

一、摘要

本文详细讲解了主成分分析法的原理及应用，包括如何通过梯度上升法求出一组数据的前n个主成分。介绍了主成分分析法如何从一个坐标系转换到另一个坐标系，通过逐步去除数据在已有主成分上的分量，求出新的主成分。具体涉及二维数据到高维数据的处理，以及如何通过编程实现主成分分析。最后，阐述了主成分分析法在降维方面的应用，并强调了该方法在数据处理和分析中的重要性。

二、主成分分析法的概述

1. 主成分分析法用于求出一组数据的第一主成分，即一个坐标轴方向，使得样本点在该轴上的方差最大。
2. 第一主成分将样本点映射到该轴上，保留了样本点之间的最大方差。
3. 对于N维数据，主成分分析法会重新排列n个轴，使得第一个轴保持最大的方差，第二个轴次之，依此类推。

三、求下一个主成分的方法

1. 求出第一主成分后，可以通过将数据在第一主成分上的分量去掉，然后求出下一个主成分。
2. 通过将样本点减去其在第一主成分上的投影，得到新的数据样本。
3. 在新数据样本上重新求第一主成分，即可得到原来的数据的第二个主成分。
4. 具体公式如下所示：

解释该图片的含义：

这是主成分分析中 “剔除第一主成分分量” 的操作示意图，核心逻辑如下：

• 主成分方向：向量 w 代表第一个主成分（方差最大的方向），是数据分布最显著的特征方向。
• 投影计算：
• 剔除主成分：

四、编程实现主成分分析法

1. 加载库和虚拟测试数据，对原始数据进行预处理。
2. 生成模拟数据：

import numpy as np
import matplotlib.pyplot as plt

X = np.empty((100, 2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100)

创建一个形状为 (100, 2) 的空数组 X，表示 100 个二维数据点。
X[:,0]：第一列数据服从 [0, 100) 的均匀分布，模拟第一个特征。
X[:,1]：第二列数据基于第一列的线性关系（0.75 * X[:,0] + 3），并添加均值为 0、标准差为 10 的正态分布噪声，模拟第二个特征与第一个特征的相关性。

3. 定义去均值函数并处理数据：

def demean(X):
    return X - np.mean(X, axis=0)
X = demean(X)

demean 函数：通过减去每列的均值（np.mean(X, axis=0)），对数据进行中心化（去均值），这是主成分分析（PCA）的预处理步骤，确保数据围绕原点分布，便于后续计算主成分。
X = demean(X)：对生成的原始数据 X 应用去均值处理。

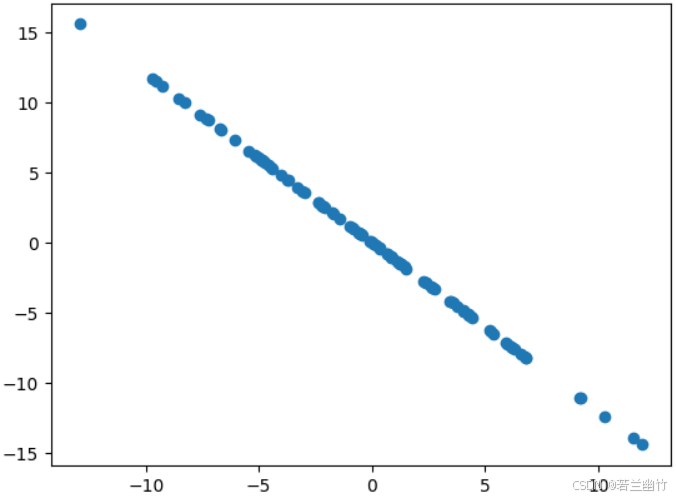
4. 可视化数据：

plt.scatter(X[:,0], X[:,1])
plt.show()

使用 plt.scatter 绘制去均值后的数据散点图，展示二维数据的分布形态，辅助观察数据特征（如是否存在线性关系），为后续主成分分析提供直观参考。

五、封装并调用主成分分析法求前n个主成分（以n取2为例）

1. 求出第一主成分，并验证推导公式的正确性。

def f(w, X):
    return np.sum((X.dot(w)**2)) / len(X)
def df(w, X):
    return X.T.dot(X.dot(w)) * 2. / len(X)
def direction(w):
    return w / np.linalg.norm(w)
def first_component(X, initial_w, eta, n_iters=1e4, epsilon=1e-8):
    w = direction(initial_w)
    cur_iter = 0
    while cur_iter < n_iters:
        gradient = df(w, X)
        last_w = w
        w = w + eta * gradient
        w = direction(w)
        if (abs(f(w, X) - f(last_w, X)) < epsilon):
            break
        cur_iter += 1
    return w

2. f(w, X) 函数：

• 作用：计算数据 ( X ) 在向量 ( w ) 方向上投影的方差（主成分分析中，方差最大化是目标）。
• 公式：先计算 ( X ) 与 ( w ) 的点积（投影值），平方后求和，再除以数据量 ( len(X) )，得到平均投影方差。

3. df(w, X) 函数：

• 作用：计算目标函数 ( f(w, X) ) 关于 ( w ) 的梯度（用于梯度上升优化）。
• 公式：通过矩阵运算推导梯度公式，最终返回梯度向量。

4. direction(w) 函数：

• 作用：对向量 ( w ) 进行归一化，确保向量长度为 1（主成分方向只需关注方向，不关注长度）。
• 实现：用 ( w ) 除以其范数（np.linalg.norm(w)）。

5. first_component(X, initial_w, eta, n_iters, epsilon) 函数：

• 作用：通过梯度上升法寻找第一个主成分（方差最大的方向）。
• 流程：
• 初始化 ( w ) 并归一化。
• 循环迭代：计算梯度，更新 ( w )，再次归一化。
• 当目标函数变化量小于 epsilon 时提前终止，最终返回第一个主成分方向 ( w )。
• 参数：
• X：输入数据（需提前去均值）；
• initial_w：初始向量；
• eta：学习率；
• n_iters：最大迭代次数；
• epsilon：收敛判断阈值。

3. 去除第一主成分的分量，求出第二主成分，并验证其与第一主成分的垂直关系。

4. 求第一个主成分的代码：

initial_w = np.random.random(X.shape[1])
eta = 0.01
w = first_component(X, initial_w, eta)

输出结果：

array([ 0.77280722,  0.63464085])

代码解释：

• 初始化向量：
• initial_w = np.random.random(X.shape[1])：生成一个随机初始向量 initial_w，维度与数据 X 的特征数（X.shape[1]，此处为 2）一致，作为梯度上升的起始点。
• 设置学习率：
• eta = 0.01：定义梯度上升的学习率 eta，控制每次参数更新的步长。
• 计算第一个主成分：
• w = first_component(X, initial_w, eta)：调用之前定义的 first_component 函数，通过梯度上升算法，在去均值后的数据 X 上，以 initial_w 为起点、eta 为学习率，求解第一个主成分（即方差最大的方向）。
• 结果输出：
• 最终得到的 w 是一个二维向量 array([ 0.77280722, 0.63464085])，表示数据 X 的第一个主成分方向，该方向能最大化数据投影的方差。

2. 去除第一主成分的计算：

# 去除第一主成分后的新数据计算
X2 = np.empty(X.shape)
for i in range(len(X)):
    X2[i] = X[i] - X[i].dot(w) * w
# 可视化新数据
plt.scatter(X2[:,0], X2[:,1])
plt.show()

• 去除第一主成分的计算：
• X2 = np.empty(X.shape)：创建与原始数据 X 形状相同的空数组 X2，用于存储去除第一主成分后的新数据。
• 循环部分：
• X[i].dot(w)：计算原始数据点 X[i] 在主成分方向 w 上的投影值。
• X[i] - X[i].dot(w) * w：从原始数据点 X[i] 中减去其在 w 方向的投影向量，得到剔除第一主成分后的新数据点 X2[i]。这一步实现了“剥离主成分信息”，使 X2 仅保留其他维度的特征。
• 可视化新数据：
• plt.scatter(X2[:,0], X2[:,1])：绘制去除第一主成分后数据 X2 的散点图，展示数据在二维平面上的分布。
• plt.show()：显示图形，直观呈现剔除主成分后的数据特征（如分布形态、离散程度变化等），辅助分析主成分对原始数据的影响。

1. 计算第二主成分：

![](https://wy-static.wenxiaobai.com/chat-rag-image/10748717979624453296)
# 计算第二主成分
w2 = first_component(X2, initial_w, eta)
w2
# 计算两主成分的点积
w.dot(w2)

输出结果：

array([-0.6346367 ,  0.77281062])  # w2 的值
5.3707849826389875e-06  # w 与 w2 的点积结果

• 计算第二主成分（w2）：
• w2 = first_component(X2, initial_w, eta)：对已剔除第一主成分的数据 X2，再次调用 first_component 函数，计算第二主成分 w2。此时，w2 是在去除第一主成分信息后，数据剩余方差最大的方向。
• 验证主成分正交性：
• w.dot(w2)：计算第一主成分 w 和第二主成分 w2 的点积。结果接近5.3707849826389875e-06（近似为 0），体现了主成分分析的核心性质：不同主成分之间相互正交。这是因为 PCA 在推导过程中，会确保后续主成分与已提取的主成分正交，从而实现特征方向的无冗余划分。

4. 通过向量化操作简化数据变换过程，提高计算效率。

• 向量化的代码实现：

# 从原始数据 X 中剔除第一主成分的信息，得到新数据 X2。
X2 = X - X.dot(w).reshape(-1, 1) * w

• 代码解释
• 核心功能：从原始数据 X 中剔除第一主成分的信息，得到新数据 X2。
• 分步解析：

1. X.dot(w)：计算原始数据 X 中每个样本在主成分方向 w 上的投影值（标量），结果是长度为样本数的一维数组。
2. .reshape(-1, 1)：将一维的投影值数组转换为列向量（形状为 (样本数, 1)），以便后续与 w 进行矩阵乘法。
3. X.dot(w).reshape(-1, 1) * w：将投影值与主成分方向向量 w 相乘，得到每个样本在 w 方向上的投影向量。
4. X - ...：从原始数据 X 中减去投影向量，最终得到剔除第一主成分信息后的数据 X2，此时 X2 仅保留其他主成分相关的特征。
   这行代码通过向量化操作，简洁高效地实现了主成分分析中“去除第一主成分分量”的核心逻辑，相比循环计算（如前文用 for 循环逐样本处理），运算效率更高。

六、小结：PCA 的应用与方差的作用

6.1 PCA应用步骤

1. 数据预处理：即标准化数据
2. 计算主成分：对高维向量进行PCA，找到方差最大的方向（主成分）。先找到第一个主成分，然后再找到第二个主成分，依此类推。
3. 保留方差最大的主成分：选择前 K 个主成分（例如 K=50），覆盖 95% 以上的总方差。
4. 降维与重构：将原始N维的向量投影到前 K 个主成分上，得到 K 维的低维表示。通过这 K 个主成分，可以重构出近似的数据集。

6.2 方差最大的实际意义

1. 信息保留：方差最大的主成分（例如前n个）保留了原始数据集中最显著的特征，而方差较小的主成分可能对应噪声或细节。
2. 降维效果：原始数据需要n维存储，而通过 PCA 只需 低维（如50维）即可表达 95% 的信息。
3. 应用价值：

• 人脸识别：通过低维的主成分表示，快速比对两张人脸的特征差异。
• 数据压缩：存储或传输时只需保留主成分权重，而非全部像素。
• 去噪：忽略方差小的成分（噪声），提升模型鲁棒性。

6.3 结论

通过保留方差最大的主成分，PCA 在保留关键信息的前提下，显著降低了数据维度。