算法详解：单调栈的概念、应用及经典例题

算法详解：单调栈的概念、应用及经典例题

引用

CSDN

1.

https://m.blog.csdn.net/rzsh1234/article/details/146124812

单调栈是一种特殊的栈结构，它在保持“先进后出”规则的同时，要求栈内的元素从栈底到栈顶是单调递增或单调递减的。这种特性使得单调栈在处理某些特定问题时非常高效，特别是在需要寻找某个元素的前后最近的更大或更小元素的场景中。本文将详细介绍单调栈的概念、应用场景以及一个经典例题的解决方案。

单调栈简介

单调栈不是一种新的数据结构，它在结构上仍然是一个普通栈，只是在使用方法上有所区别。在栈的「先进后出」规则基础上，要求「从 栈底 到 栈顶 的元素是单调递增（或者单调递减）」。其中满足从栈底到栈顶的元素是单调递增的栈，叫做「单调递增栈」。满足从栈底到栈顶的元素是单调递减的栈，叫做「单调递减栈」。

单调栈的核心思想是：及时去掉无用数据，保证栈中数据有序。

单调栈的应用

1. 寻找当前元素左侧，离它最近，并且比它大的元素在哪

从左往右遍历元素，构造一个单调递减的栈。插入当前位置的元素时：

• 如果栈为空，则左侧不存在比当前元素大的元素；
• 如果栈非空，插入当前位置元素时的栈顶元素就是所找的元素。

因为我们要找的是最终结果的位置。因此，栈里存的是每个元素的下标。

以数组a[]为例：

a[] = {1,4,10,6,3,3,15,21,8}

• 栈顶元素小于等于待插入元素 st.top() <= a[i]
• 操作：删除栈顶元素
• 栈顶元素一定不是当前元素要找的数
  （因为要找比自己大的元素，栈顶元素小于当前元素肯定不可以了）
• 栈顶元素必定不是后面元素要找的数
  （栈顶元素都小于待插入元素了，从左往右遍历，就算后面元素要找比自己大的元素，离自己最近的也不会是栈顶元素，待插入元素比栈顶元素更近）
• 如果栈顶元素大于待插入元素 st.top() > a[i]
• 操作：更新结果
• 栈顶元素就是i位置要找的数
• 把当前元素加入栈中

模版：

#include <iostream>
#include <stack>
using namespace std;
const int N = 3e6 + 10;
int a[N], n;
int ret[N];
void test()
{
    stack<int> st; //维护一个单调递减的栈，栈里存的是元素的下标
    for (int i = 1;i <= n;i++)
    {
        while(st.size() && a[st.top()] <= a[i]) 
            st.pop();
        if (st.size()) 
            ret[i] = st.top();
        st.push(i);
    }
}
int main()
{
    cin >> n;
    for (int i = 1;i <= n;i++) cin >> a[i];
    test();
    for (int i = 1;i <= n;i++) cout << ret[i]<<" ";
    return 0;
}

2. 寻找当前元素左侧，离它最近，并且比它小的元素在哪

从左往右遍历元素，构造一个单调递增的栈。插入当前位置的元素时：

• 如果栈为空，则左侧不存在比当前元素小的元素；
• 如果栈非空，插入当前位置元素时的栈顶元素就是所找的元素。

同理：

• 栈顶元素大于等于待插入元素 st.top() >= a[i]
• 操作：删除栈顶元素
• 栈顶元素一定不是当前元素要找的数
  （因为要找比自己小的元素，栈顶元素大于等于当前元素肯定不可以了）
• 栈顶元素必定不是后面元素要找的数
  （栈顶元素都大于待插入元素了，从左往右遍历，就算后面元素要找比自己小的元素，离自己最近的也不会是栈顶元素，待插入元素比栈顶元素更近）
• 如果栈顶元素大于待插入元素 st.top() < a[i]
• 操作：更新结果
• 栈顶元素就是i位置要找的数
• 把当前元素加入栈中

模版：

#include <iostream>
#include <stack>
using namespace std;
const int N = 3e6 + 10;
int a[N], n;
int ret[N];
void test()
{
    stack<int> st; //维护一个单调递减的栈，栈里存的是元素的下标
    for (int i = 1;i <= n;i++)
    {
        while(st.size() && a[st.top()] >= a[i]) 
            st.pop();
        if (st.size()) 
            ret[i] = st.top();
        st.push(i);
    }
}
int main()
{
    cin >> n;
    for (int i = 1;i <= n;i++) cin >> a[i];
    test();
    for (int i = 1;i <= n;i++) cout << ret[i]<<" ";
    return 0;
}

3. 寻找当前元素右侧，离它最近，并且比它大的元素在哪

与应用一类似，仅需改变遍历顺序，从右往左遍历，创建单调递减的栈

模版：

#include <iostream>
#include <stack>
using namespace std;
const int N = 3e6 + 10;
int a[N], n;
int ret[N];
void test()
{
    stack<int> st; //维护一个单调递减的栈，栈里存的是元素的下标
    for (int i = n;i >= 1;i--)
    {
        while(st.size() && a[st.top()] <= a[i]) 
            st.pop();
        if (st.size()) 
            ret[i] = st.top();
        st.push(i);
    }
}
int main()
{
    cin >> n;
    for (int i = 1;i <= n;i++) cin >> a[i];
    test();
    for (int i = 1;i <= n;i++) cout << ret[i]<<" ";
    return 0;
}

4. 寻找当前元素右侧，离它最近，并且比它小的元素在哪

与应用2类似，仅需改变遍历顺序，从右往左遍历，创建单调递增的栈

#include <iostream>
#include <stack>
using namespace std;
const int N = 3e6 + 10;
int a[N], n;
int ret[N];
void test()
{
    stack<int> st; //维护一个单调递减的栈，栈里存的是元素的下标
    for (int i = n;i >= 1;i--)
    {
        while(st.size() && a[st.top()] >= a[i]) 
            st.pop();
        if (st.size()) 
            ret[i] = st.top();
        st.push(i);
    }
}
int main()
{
    cin >> n;
    for (int i = 1;i <= n;i++) cin >> a[i];
    test();
    for (int i = 1;i <= n;i++) cout << ret[i]<<" ";
    return 0;
}

总结：

• 找左侧，正遍历；找右侧，逆遍历；
• 比它大，单调减；比它小，单调增；

经典例题

最大矩形面积问题

思路：
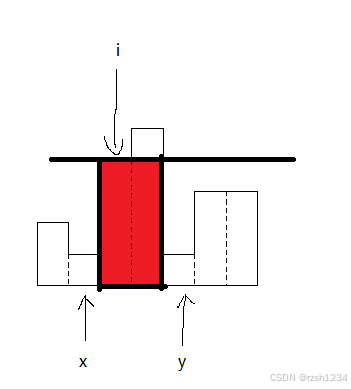
最后大矩形的上边界一定是某个小矩形的顶
那么我们就枚举每一个小矩形,将其顶作为限制条件尽可能地向两边扩展
我们枚举每一个小矩形i，如上图，枚举到 i 位置时，向左找离它最近的且比它小的值， 记录所在位置x，再向右找离它最近且最小的值，记录所在位置y 。大矩形的面积就是图示红色的部分。
面积为 i 位置小矩形的高度 乘以 宽度(y-x+1)。
所以用单调栈就可以解决，代码如下

#include<iostream>
#include<stack>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
LL n;
LL h[N],x[N],y[N];
![](https://wy-static.wenxiaobai.com/chat-rag-image/4811864681375557130)
int main()
{
    while (cin >> n && n)
    {
        for (int i = 1;i <= n;i++)
        {
            cin >> h[i];
        }
        // 找左边第一个比自己小
        stack<LL> st;
        for (int i = 1;i <= n;i++)
        {
            while (st.size() && h[st.top()] >= h[i])
                st.pop();
            if (st.size())
                x[i] = st.top();
            else
                x[i] = 0;
            st.push(i);
        }
        
        while (st.size()) st.pop(); //清空栈内数据
        // 找右边第一个比自己小
        for (int i = n;i >= 1;i--)
        {
            while (st.size() && h[st.top()] >= h[i])
                st.pop();
            if (st.size())
                y[i] = st.top();
            else
                y[i] = n+1;  
            st.push(i);
        }
        LL ret = -1;
        for (int i = 1;i <= n;i++)
        {
            ret = max(ret, h[i] * (y[i] - x[i] - 1));
        }
        cout << ret << endl; 
    }
    return 0;
}