数字电路基础知识：四种乘法器设计方法详解

数字电路基础知识：四种乘法器设计方法详解

引用

CSDN

1.

https://blog.csdn.net/vivid117/article/details/100926131

乘法器是数字信号处理和数字通信中的关键组件，其设计方法直接影响系统的性能和资源消耗。本文将详细介绍四种常见的乘法器设计方法：并行乘法器、移位相加乘法器、查找表乘法器和加法树乘法器。每种方法都有其独特的优缺点和适用场景，通过对比分析，读者可以更好地理解如何根据具体需求选择合适的乘法器设计方案。

一、并行乘法器

并行乘法器在Verilog中可以直接使用乘法运算符（*）来实现。这种方法虽然简单，但通常会生成效率较低的硬件结构。

特点

• 由乘法运算符描述，由EDA软件综合
• 运算速度快，但耗用资源多

示例代码：8位并行乘法器

module multi(a,b,c);
parameter size = 8;
input [size-1:0] a,b;
output [2*size-1:0] c; 	//输出位宽
assign c = a*b;
endmodule

二、移位相加乘法器

移位相加乘法器通过判断被乘数的每一位，决定是否将乘数左移后与当前结果相加。这种方法主要由移位运算和加法运算构成。

优点

• 占用资源较少，适合低速信号处理

缺点

• 串行乘法器的速度比较慢，需要更多的时钟周期

关键算法

module multi_shift(a,b,c);  //不可综合提供算法
parameter size = 8;
input [size-1:0] a,b;
output [2*size-1:0] c; 	//输出位宽
reg[2*size-1:0] c;
integer i;
always@(a or b)
begin
    c=0;
    for (i=1; 1<=size;i=i+1) begin
        c = c + ((b[i] == 1)? (a<<[i-1]):0); 	//移位相加
    end
end
endmodule

三、查找表乘法器

查找表乘法器预先存储所有可能的乘法结果，通过输入数据作为地址来查找对应的结果。这种方法速度很快，但需要占用较多的存储资源。

特点

• 速度取决于读取存储器的速度
• 面积换取速度的思想体现
• 适用于位宽较小的情况

设计思路

• 对于四位查找表：A1 高两位, A2低两位
• 对于八位查找表：A1 高四位, A2低四位

示例代码：2位查找表乘法器

module lookup22(dina,dinb,dout,clk);
input [1:0] dina,dinb;
input clk;
output [3:0] dout;
reg [3:0] dout;
always @ ( posedge clk )
begin
   case({dina,dinb})
      4'b0000:dout<=0;
      4'b0001:dout<=0;
      4'b0010:dout<=0;
      4'b0011:dout<=0;
      4'b0100:dout<=0;
      4'b0101:dout<=1;
      4'b0110:dout<=2;
      4'b0111:dout<=3;
      4'b1000:dout<=0;
      4'b1001:dout<=2;
      4'b1010:dout<=4;
      4'b1011:dout<=6;
      4'b1100:dout<=0;
      4'b1101:dout<=3;
      4'b1110:dout<=6;
      4'b1111:dout<=9;
      default: dout<=4'dx;
   endcase 
end   
endmodule

扩展到4位查找表乘法器

module lookup44(dina,dinb,dout,clk);
input [3:0] dina,dinb;
input clk;
output [7:0] dout;
reg [7:0] dout;
reg [1:0] a1,a2; 	//操作数高2位
reg [1:0] b1,b2;	//操作数低2位
wire [3:0] dout1,dout2,dout3,dout4;		//乘积每两位一组
//输入数据拆为高2位和低2位分别缓存
always @ ( posedge clk )
begin
   a1<=dina[3:2]; a2<=dina[1:0];
   b1<=dinb[3:2]; b2<=dinb[1:0];
end    
//调用2位查找表乘法器
lookup22 mul1(a1,b1,dout1,clk),
         mul2(a2,b1,dout2,clk),
         mul3(a1,b2,dout3,clk),
         mul4(a2,b2,dout4,clk);
         
//将4个乘法运算的结果相加输出
always @ ( posedge clk )
begin
   dout<=(dout1<<4)+(dout2<<2)+(dout3<<2)+dout4;
end  
endmodule

四、加法树乘法器

加法树乘法器通过构建加法树结构，能够在单个时钟周期内完成乘法运算。

实现示例：8位加法树乘法器

module multi_add_tree(a,b,clk,out);
output [15:0] out;
input [7:0] a,b;
input clk;
wire [15:0] out;
wire [15:0] out1,c1;
wire [13:0] out2;
wire [11:0] out3.c2;
wire [9:0] out4;
reg [14:0] temp0; 
reg [13:0] temp1;
reg [12:0] temp2;
reg [11:0] temp3;
reg [10:0] temp4;
reg [9:0] temp5;
reg [8:0] temp6;
reg [7:0] temp7;
// 8*1乘法器
function [7:0] mut8_1;
input [7:0] operand;
input sel;
begin
    mut8_1 = sel ? operand : 8'b0000_0000;
end
endfunction 
//操作数b各位与操作数a相乘
always @(posedge clk)
begin
    temp7 = mut8_1(a,b[0]);
    temp6 = (mut8_1(a,b[1]))<<1;
    temp5 = (mut8_1(a,b[2]))<<2;
    temp4 = (mut8_1(a,b[3]))<<3;
    temp3 = (mut8_1(a,b[4]))<<4;
    temp2 = (mut8_1(a,b[5]))<<5;
    temp1 = (mut8_1(a,b[6]))<<6;
    temp0 = (mut8_1(a,b[7]))<<7;
end
//加法树运算
assign out1 = temp0 + temp1;
assign out2 = temp2 + temp3;
assign out3 = temp4 + temp5;
assign out4 = temp6 + temp7;
assign c1 = out1 + out2;
assign c1 = out3 + out4;
assign out = c1 + c2;
endmodule

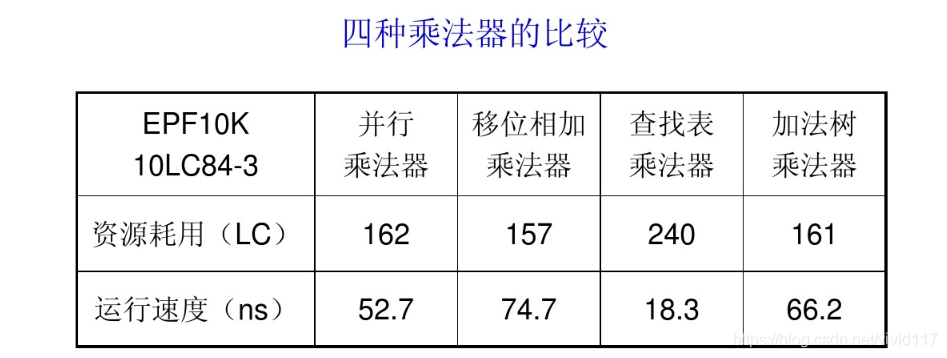
五、四种乘法器比较

四种乘法器在资源占用和运行速度方面各有优劣：

六、乘累加器

乘累加器可以在一个时钟周期内完成一次乘法运算，并在下一个时钟周期将结果累加。

示例代码：8位乘累加器

module MAC(a, b, out, clk, clr);
output [15:0] out;
input [7:0] a, b;
input clk, clr;
wire [15:0] sum;
reg [15:0] out;
function [15:0] mult;
input [7：0] a,b;
reg [15:0] result;
integer i;
begin
![](https://wy-static.wenxiaobai.com/chat-rag-image/2309766104589724497)
    result = a[0]? b :0;
    for (i=1; i<= 7;i=i+1)
        begin
         result = result + ((a[i] == 1)?  (b<<(i-1)): 0); 	//移位相加
        end
    mult = result;
end
endfunction
assign sum = mult(a,b) + out;
always@(posedge clk or posedge clr)
begin
    if(clr) out <= 0;
    else out <= sum;
end
endmodule

通过对比分析这四种乘法器的设计方法，读者可以更好地理解如何根据具体应用场景和需求选择合适的乘法器设计方案。无论是追求速度、资源效率还是灵活性，本文提供的方案都能为数字电路设计提供有价值的参考。