KNN算法详解：从基础原理到KDTree优化

KNN算法详解：从基础原理到KDTree优化

引用

CSDN

1.

https://blog.csdn.net/u013850277/article/details/87993174

KNN（K近邻）算法是一种经典的监督学习算法，广泛应用于分类和回归问题。本文将从KNN算法的基本概念出发，详细讲解其原理、实现方法以及KDTree优化技术，帮助读者全面理解这一重要算法。

前言：什么是KNN算法

• KNN全称K-nearest neighbors，是一种典型的监督学习算法。
• 通俗地讲，K近邻算法是将待预测的样本置入到数据集中，然后通过与它最靠近的K个样本来代表待预测的样本。
• 这个思想类似于“物以类聚，人以群分”，一个人的收入可以通过与他经常交往的五个人收入的平均数来确定。
• KNN算法既可以应用于分类应用中，也可以应用在回归应用中。在分类预测时，一般采用多数表决法；而在做回归预测时，一般采用平均值法。

一、KNN算法原理

1. 从训练集合中获取K个离待预测样本距离最近的样本数据；
2. 根据获取得到的K个样本数据来预测当前待预测样本的目标属性值。

简单Demo说明

如上图中，绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？

若K=3，意思是获取3个离待测样本距离最近的数据来预测当前待预测的目标属性。

当取3个最近邻样本数据时，红色三角形所占比例为2/3，蓝色四方形占比例为1/3，因此绿色圆将被赋予红色三角形那个类；

同理，若K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。

• 由上述Demo可知，对于KNN算法来说有三个比较重要的因素要考虑，分别如下所述：

KNN 算法三要素

1. K值的选择：K值的确定与样本最终的判定结果有很大的关系；K 值太小会使得 KNN 算法容易过拟合。反之，太大则会欠拟合。因此，一般采用交叉验证的方式选取 K 值。

2. 距离的度量：通过什么样的距离理论确定最近邻的样本数据。一般使用欧氏距离(欧几里得距离)；

3. 决策规则：以什么样的决策规则来确定最终的输出结果。如上图的决策规则是通过“多数表决法”对结果进行分类。在分类预测时，一般采用“多数表决法”或“加权多数表决法”；而在做回归预测时，一般采用“平均值法”或“加权平均值法”，这也是KNN做分类与回归最主要的区别。这里所说的加权一般情况下采用权重和距离成反比的方式来计算。

二、KNN 简单编码样例

from sklearn import neighbors
from sklearn import datasets
from sklearn.model_selection import train_test_split

iris = datasets.load_iris()
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=0)

KNN = neighbors.KNeighborsClassifier(algorithm='kd_tree', n_neighbors=3)
KNN.fit(x_train, y_train)

print("训练集预测的准确率：", KNN.score(x_train, y_train))
print("测试集预测的准确率: ", KNN.score(x_test, y_test))
print("predict: ", KNN.predict([[7, 5, 2, 0.5], [7.5, 4, 7, 2]]))

代码解说：

from sklearn import neighbors
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.externals import joblib

# 加载数据集
iris = datasets.load_iris()

# random_state 随机数种子，就是为了保证程序每次运行都分割一样的训练集合测试集。
# 如果没有给定种子，该函数默认为none，则每次分割的出来的数据集都不一样，
# 这样模型在每次运行后的结果都不一样，难以调参。
# test_size = 0.2 切割20% 的数据做为测试集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.20, 
   random_state=0)

KNN = neighbors.KNeighborsClassifier(algorithm='kd_tree', leaf_size=30,
   metric='minkowski', n_neighbors=5, p=2,weights='uniform')

# 参数说明：
# 1.weights 样本权重，可选参数: uniform(等权重)、
#    distance(权重和距离成反比，越近影响越强)；默认为uniform
# 2.n_neighbors 邻近数目，默认为5
# 3.algorithm  计算方式，默认为auto，可选参数: auto、ball_tree、kd_tree、brute；
#       如果设定为‘auto’，系统会根据传给fit方法的参数来选择最合适的算法，推荐选择kd_tree。
# 4.leaf_size  在使用KD_Tree的时候，叶子数量，默认为30,
# 5. metric  样本之间距离度量公式，默认为minkowski（闵可夫斯基）；
#     当参数p为2的时候，其实就是欧几里得距离
# 6.p 给定minkowski距离中的p值，默认为2

# 训练模型
KNN.fit(x_train, y_train)

# 将训练模型保存至本地
joblib.dump(KNN, 'KNN_MODEL.m')

# 将保存在本地的训练模型调出用于预测
KNN = joblib.load('KNN_MODEL.m')

# 输出模型训练集预测的准确率
print("训练集预测的准确率：", KNN.score(x_train, y_train))

# 输出模型测试集预测的准确率
print("测试集预测的准确率: ", KNN.score(x_test, y_test))
print("predict: ", KNN.predict([[7, 5, 2, 0.5], [7.5, 4, 7, 2]]))

• sklearn 部分样例数据

{
'data': array([[5.1, 3.5, 1.4, 0.2],
      ....
      ....
       [6.3, 2.5, 5. , 1.9],
       [6.5, 3. , 5.2, 2. ],
       [6.2, 3.4, 5.4, 2.3],
       [5.9, 3. , 5.1, 1.8]]), 
       'target': array([
       0, 0, 0, 0, 0, 0, 0, 0,
       1, 1, 1, 1, 1,
       2, 2, 2, 2, 2, 2, 2]),
        'target_names': array(['setosa', 'versicolor', 'virginica'],
        dtype='<U10'), 
       }

闵可夫斯基距离

• 闵可夫斯基距离不是一种距离，而是一类距离的定义。
• 对于 n 维空间中的两个点,假设数值点 A(x1,x2,x3,…xk), 数值点B(y1,y2,y3…yk), 则这两点的闵可夫斯基距离公式如下：
• 其中 p 是一个可变参数：
• 当 p=1 时，被称为曼哈顿距离；
• 当 p=2 时，被称为欧氏距离；
• 当 p= 无穷大时，被称为切比雪夫距离。

三、KNN算法的算法优缺点与适用场景

优点：

1. 简单，易于实现，无需估计参数，无需训练；
2. 既可以用来做分类也可以用来做回归；
3. 训练时间复杂度为O(n)；
4. 准确度高，对数据没有假设，对outlier不敏感；

缺点：

1. 懒惰算法，对测试样本分类时的计算量大，内存开销大；
2. 样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少）;
3. 可解释性较差，无法给出决策树那样的规则。

• 注：
  懒惰算法可以如此理解：训练数据并没有形成一个“模型”，而是一个新的数据需要分类了，去和所有训练数据逐一比较，最终给出分类。也可理解成延迟计算，有点类似Spark 中的 RDD，表达式不在它被绑定到变量之后就立即求值，而是在该值被取用的时候求值。

改进算法 :
待补充

四、KNN 算法的核心：KDTree

• 通过以上的分析，我们知道 KNN 分类算法的思想非常简单，它采用的就是 K 最近邻多数投票的思想。所以，算法的关键就是在给定的距离度量下，对预测实例如何准确快速地找到它的最近的 K 个邻居？也就是说在预测实例时，怎么样可以使搜索次数减少。常用的方式以下有两种：

蛮力实现(brute)：

• 计算预测样本到所有训练集样本的距离，然后选择最小的 k个距离即可得到K个最邻近点。缺点在于当特征数比较多、样本数比较多的时候，算法的执行效率比较低;

KD树(kd_tree)：

• KD树算法中，首先是对训练数据进行建模，构建KD树，然后再根据建好的模型来获取邻近样本数据。这么做的本质是使用特殊的数据结构存储训练数据，用来减少预测时的搜索次数。

KDTree 原理说明：

• 假设数据集为 M ，样本量为m个，特征维度为n, 利用M进行构建KD Tree步骤如下：

1. 根节点的选择

• 分别计算n个特征数值所对应的方差，取方差最大那个特征(设该维特征为L)做为根节点对应的维度。将L维特征的取值进行排序，取其中位数对应的数据点作为该维的根节点。
• 注：选择方差大的维度做为根节点的原因是，该维度根节点大说明数据的分离程度大，利用它来做根节点可以更加快速将数据区分开来）

2. 构建左右子树

• 对于L维小于根节点的样本划分到左子树，对于大于等于该值的样本划分到右子树。

3. 迭代生成叶子节点

• 对左右子树按步骤1，2 进行迭代，采用同样的方式找方差最大的特征作为根节点，递归即可产生KD树。

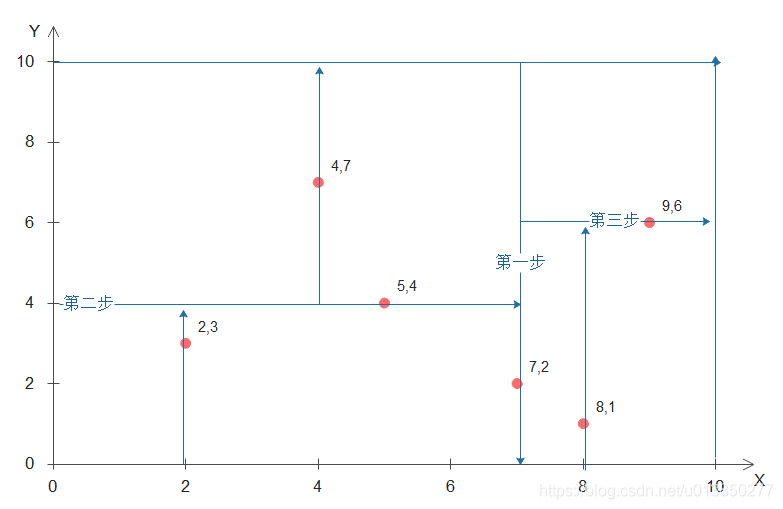
简单demo 描述KD tree的构建：
假设二维样本: {(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}

• 计算 x 与 y 维度方差

arr3 = np.array([[2, 3], [5, 4], [9, 6], [4, 7], [8, 1], [7, 2]])
print('各维方差：%s ' % (np.std(arr3, axis=0)) ** 2)
print("对x维排序：%s, x 维中位数: %s " % (np.sort(arr3[:,0]),np.median(arr3[:,0])))
print("对y维排序：%s, y 维中位数: %s " % (np.sort(arr3[:,1]),np.median(arr3[:,1])))

打印结果如下：

各维方差：[5.80555556 4.47222222] 
对x维排序：[2 4 5 7 8 9], x 维中位数: 6.0 
对y维排序：[1 2 3 4 6 7], y 维中位数: 3.5 

由于 x 维方差比 y 维的大，故选择 x 维做为根节点的分割维度；
由于 x 维中位数为 6.0，一般选取大的，故选择7，也就是点（7，2）被选为根节点；
切割后如上：
左子树 ：[2, 3], [5, 4], [4, 7]
右子树：[9, 6], [8, 1]

对左右子树进行重复步骤 1，2

arr4 = np.array([[2, 3], [5, 4], [4, 7]])
print('各维方差：%s ' % (np.std(arr4, axis=0)) ** 2)
print("对x维排序：%s, x 维中位数: %s " % (np.sort(arr4[:,0]),np.median(arr4[:,0])))
print("对y维排序：%s, y 维中位数: %s " % (np.sort(arr4[:,1]),np.median(arr4[:,1])))

打印结果如下：

各维方差：[1.55555556 2.88888889] 
对x维排序：[2 4 5], x 维中位数: 4.0 
对y维排序：[3 4 7], y 维中位数: 4.0 

• 同理计算得 分割维度为 y 维，根节点为[5,4]
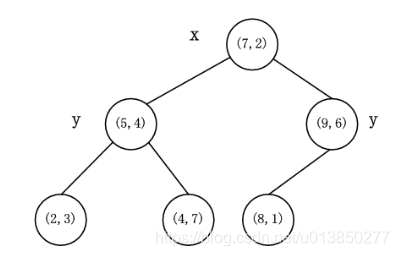
• 最终得到KD Tree 如下所示：
  上图为二维空间的划分，如果为多维则就是将线转换成面，上图转换成树结构如下所示：

4、如何通过KDTree查找最近邻点（即如何减少搜索的计算量）

• 利用 KD 树主要是可以省去对大部分数据点的搜索，从而减少搜索的计算量。
• 下面以目标点（2，4.5）来说明其搜索过程：

1. 在KD树里面找到包含目标点的叶子节点，这里找到的叶子节点分别为（7，2），（5，4），（4，7），分别计算这三个包含了目标节点的叶子节点到目标节点的距离，取其中最小的一个为半径，这里求得点（5，4）为所有叶子节点距离目标节点最小。
2. 以目标点为圆心，以步骤1中的求得的最小距离为半径，得到一个超球体，最近邻的点一定在这个超球体内部。
3. 待补充

五、模型的本地保存与调用

from sklearn import neighbors
from sklearn.externals import joblib #模型保存包
KNN = neighbors.KNeighborsClassifier(n_neighbors=3)
KNN.fit(x, y)
# 模型的本地保存
joblib.dump(KNN, "train_model.m")
![](https://wy-static.wenxiaobai.com/chat-rag-image/2546742764333469024)
# 模型的调用
![](https://wy-static.wenxiaobai.com/chat-rag-image/7951487309108540498)
from sklearn.externals import joblib #模型保存包
KNN = joblib.load("train_model.m")
print("predict: ", KNN.predict([[7, 5, 2, 0.5], [7.5, 4, 7, 2]]))