KAN神经网络：基于Kolmogorov-Arnold表示定理的新型神经网络架构

创作时间:

作者:

@小白创作中心

KAN神经网络：基于Kolmogorov-Arnold表示定理的新型神经网络架构

引用

CSDN

https://blog.csdn.net/2303_77200324/article/details/146997905

KAN神经网络（Kolmogorov–Arnold Networks）是一种基于Kolmogorov-Arnold表示定理的新型神经网络架构。该定理指出，任何多元连续函数都可以表示为有限个单变量函数的组合。与传统多层感知机（MLP）不同，KAN通过可学习的激活函数和结构化网络设计，在函数逼近效率和可解释性上展现出潜力。

一、引言

KAN神经网络（Kolmogorov–Arnold Networks）是一种基于Kolmogorov-Arnold表示定理的新型神经网络架构。该定理指出，任何多元连续函数都可以表示为有限个单变量函数的组合。与传统多层感知机（MLP）不同，KAN通过可学习的激活函数和结构化网络设计，在函数逼近效率和可解释性上展现出潜力。

二、技术与原理简介

1.Kolmogorov-Arnold 表示定理

Kolmogorov-Arnold 表示定理指出，如果是有界域上的多元连续函数，那么它可以写为单个变量的连续函数的有限组合，以及加法的二进制运算。更具体地说，对于光滑
其中和。从某种意义上说，他们表明唯一真正的多元函数是加法，因为所有其他函数都可以使用单变量函数和 sum 来编写。然而，这个 2 层宽度 - Kolmogorov-Arnold 表示可能不是平滑的由于其表达能力有限。我们通过以下方式增强它的表达能力将其推广到任意深度和宽度。
，

2.Kolmogorov-Arnold 网络（KAN）

Kolmogorov-Arnold 表示可以写成矩阵形式
其中
我们注意到和都是以下函数矩阵（包含输入和输出）的特例，我们称之为 Kolmogorov-Arnold 层：
其中
。

定义层后，我们可以构造一个 Kolmogorov-Arnold 网络只需堆叠层！假设我们有层，层的形状为。那么整个网络是
相反，多层感知器由线性层和非线错：
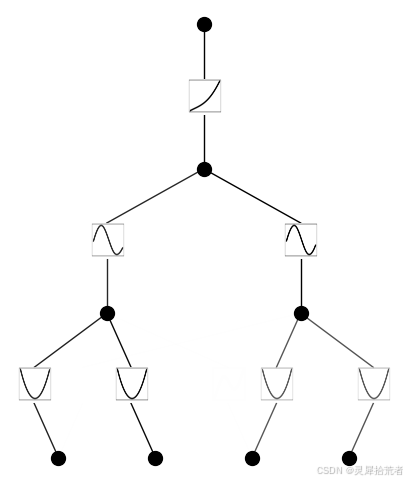
KAN 可以很容易地可视化。（1） KAN 只是 KAN 层的堆栈。（2）每个 KAN 层都可以可视化为一个全连接层，每个边缘上都有一个1D 函数。

三、代码详解

原始的Kolmogorov-Arnold定理指出，仅需两层函数组合（内层和外层函数）就足够了，但这些函数可能并非光滑，甚至可能是分形的。我们将KA表示推广到任意深度。一个两层KAN（带有光滑激活函数）无法处理的例子是：
，这需要至少三层KAN。

from kan import KAN, create_dataset
import torch
# create a KAN: 2D inputs, 1D output, and 5 hidden neurons. cubic spline (k=3), 5 grid intervals (grid=5).
model = KAN(width=[4,2,1,1], grid=3, k=3, seed=0)
f = lambda x: torch.exp((torch.sin(torch.pi*(x[:,[0]]**2+x[:,[1]]**2))+torch.sin(torch.pi*(x[:,[2]]**2+x[:,[3]]**2)))/2)
dataset = create_dataset(f, n_var=4, train_num=3000)
# train the model
model.train(dataset, opt="LBFGS", steps=20, lamb=0.001, lamb_entropy=2.);
model.plot(beta=10)

  
# it seems that removing edge manually does not change results too much. We include both for completeness.
![](https://wy-static.wenxiaobai.com/chat-rag-image/3845844110143144727)
remove_edge = True
if remove_edge == True:
    model.remove_edge(0,0,1)
    model.remove_edge(0,1,1)
    model.remove_edge(0,2,0)
    model.remove_edge(0,3,0)
else:
    pass

  
grids = [3,5,10,20,50]
#grids = [5]
train_rmse = []
test_rmse = []
for i in range(len(grids)):
    model = KAN(width=[4,2,1,1], grid=grids[i], k=3, seed=0).initialize_from_another_model(model, dataset['train_input'])
    results = model.train(dataset, opt="LBFGS", steps=50, stop_grid_update_step=30);
    train_rmse.append(results['train_loss'][-1].item())
    test_rmse.append(results['test_loss'][-1].item())

  
import numpy as np
import matplotlib.pyplot as plt
n_params = np.array(grids) * (4*2+2*1+1*1)
plt.plot(n_params, train_rmse, marker="o")
plt.plot(n_params, test_rmse, marker="o")
plt.plot(n_params, 10000*n_params**(-4.), color="black", ls="--")
plt.legend(['train', 'test', r'$N^{-4}$'], loc="lower left")
plt.xscale('log')
plt.yscale('log')
print(train_rmse)
print(test_rmse)

四、总结与思考

KAN神经网络通过融合数学定理与深度学习，为科学计算和可解释AI提供了新思路。尽管在高维应用中仍需突破，但其在低维复杂函数建模上的潜力值得关注。未来可能通过改进计算效率、扩展理论边界，成为MLP的重要补充。

1. KAN网络架构

关键设计：可学习的激活函数：每个网络连接的“权重”被替换为单变量函数（如样条、多项式），而非固定激活函数（如ReLU）。分层结构：输入层和隐藏层之间、隐藏层与输出层之间均通过单变量函数连接，形成多层叠加。参数效率：由于理论保证，KAN可能用更少的参数达到与MLP相当或更好的逼近效果。
示例结构：输入层 → 隐藏层：每个输入节点通过单变量函数

连接到隐藏节点。隐藏层 → 输出层：隐藏节点通过另一组单变量函数
组合得到输出。