路径规划——广度优先搜索与深度优先搜索

路径规划——广度优先搜索与深度优先搜索

引用

CSDN

1.

https://blog.csdn.net/weixin_51995147/article/details/140859864

在图论中，广度优先搜索（BFS）和深度优先搜索（DFS）是最基本的两种图遍历算法。它们在很多领域都有广泛的应用，比如路径规划、网络爬虫、连通性检测等。本文将详细介绍这两种算法的原理、实现方法，并通过具体的代码示例帮助读者理解。

路径规划——广度优先搜索与深度优先搜索

1.广度优先搜索 Breath-First-Search

在图论中也称为广度优先遍历，类似于树的层序遍历。

算法原理

从起始节点出发，首先访问它的邻近节点，然后依次访问这些邻近节点的邻近节点，直到所有节点都被访问到。广度优先搜索是从一个起始节点开始逐层地访问所有节点的。

广度优先搜索是一种图遍历算法，每向前走一步可能访问一批顶点，不像深度优先搜索那样有回退的情况，因此它不是一个递归的算法。为了实现逐层的访问，算法必须借助一个辅助队列，以记忆正在访问的顶点的下一层顶点。

现有如下节点图Graph，要求从A点开始搜索，搜索全部节点，将节点搜索序列作为结果输出。

将上图整理得下图

那么整个广度优先搜索的过程如下图：

算法实现

from collections import deque

def bfs(graph, start):
    # 初始化队列，并将起始节点加入队列
    queue = deque([start])
    # 初始化访问顺序列表
    visited = [start]
    while queue:
        # 取出队列中的当前节点
        current = queue.popleft()
        
        # 遍历当前节点的所有邻居节点
        for neighbor in graph[current]:
            if neighbor not in visited:  # 如果邻居节点尚未被访问
                # 将邻居节点加入队列
                queue.append(neighbor)
                # 记录访问顺序
                visited.append(neighbor)
    return visited

# 示例图的定义
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

# 使用BFS算法
start_node = 'A'
visited = bfs(graph, start_node)
print(f"Visit order: {visited}")

寻找在上图中A->E的最短路径：

from collections import deque

def bfs(graph, start, goal):
    # 初始化队列，并将起始节点加入队列
    queue = deque([start])
    # 初始化访问顺序列表
    visited = [start]
    # 初始化父节点集合
    previous = {start: None}
    while queue:
        # 取出队列中的当前节点
        current = queue.popleft()
        if current == goal:
            break
        
        # 遍历当前节点的所有邻居节点
        for neighbor in graph[current]:
            if neighbor not in visited:  # 如果邻居节点尚未被访问
                # 将邻居节点加入队列
                queue.append(neighbor)
                # 记录访问顺序
                visited.append(neighbor)
                # 将当前节点保存为邻节点的父节点
                previous[neighbor] = current
    path = []
    current = goal
    # Find the full path by backtracking
    while current is not None:
        path.append(current)
        current = previous.get(current)
    path = path[::-1]
    distance = len(path)-1
    return path,distance

# 示例图的定义
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

# 使用BFS算法
start = 'A'
goal = 'E'
path,distance = bfs(graph, start, goal)
print("Distance: ",distance)
print(f"Short path: {path}")

输出结果：

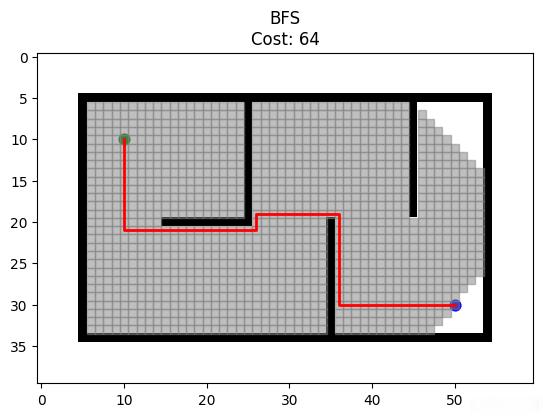
利用BFS算法寻找栅格地图中两点之间的最短路径的代码实现如下：

from collections import deque
import numpy as np

class BFS:
    def __init__(self, grid, board_size, start, goal):
        self.grid = grid
        self.board_size = board_size
        self.start = start
        self.goal = goal

    def plan(self):
        """
            Use BFS algorithm to plan path in grid map.
            Since the cost between every two neighbouring nodes is 1 which is different from Dijkstra,
            only four directions including up, right, down, left are allowed
        
        """
        visited = set() # Used to mark nodes that are visited
        self.searched = [] # Used to record nodes that are searched
        previous_nodes = {self.start: None}
        que = deque([self.start])
        visited.add(self.start)
        while que:
            # Select the node closest to the start node
            current_node = que.popleft()
            # Append the current node into searched nodes
            self.searched.append(current_node)
            
            # Break when the current node is the goal
            if current_node == self.goal:
                break
            
            # Find the neighbors of the current node and determine in turn if they have already been visited
            neighbors = self.get_neighbors(current_node)
            for neighbor in neighbors:
                # If the current node has been visited, skip it
                if neighbor in visited:
                    continue
                previous_nodes[neighbor] = current_node
                que.append(neighbor)
                visited.add(neighbor) # mark the neighbor is visited
        
        self.path = []
        current_node = self.goal
        # Find the full path by backtracking
        while current_node is not None:
            self.path.append(current_node)
            current_node = previous_nodes.get(current_node)
        self.path = self.path[::-1]
        return len(self.path)-1

    def get_neighbors(self, node):
        neighbors = []
        next_directions = [(1,0),(0,-1),(-1,0),(0,1)]
        for next_d in next_directions:
            neighbor = (node[0] + next_d[0], node[1] + next_d[1])
            if self.board_size <= neighbor[0] < len(self.grid)-self.board_size and self.board_size <= neighbor[1] < len(self.grid[0])-self.board_size:
                if self.grid[neighbor[0]][neighbor[1]] == 0:
                    neighbors.append(neighbor)
        return neighbors

2.深度优先搜索 Depth-First-Search

在树和图论的数据结构中也称为深度优先遍历。

算法原理

从起始节点出发，沿着一个分支深入到尽可能深的节点，然后回溯并继续访问其他分支。这种"走到尽头再返回"的算法范式通常是基于递归来实现的。

同样以上述例子为例，整个深度优先搜索的过程如下：

算法实现

from collections import deque

def dfs(graph, current_node, visited):
    visited.append(current_node)
    
    # 遍历当前节点的所有邻居节点
    for neighbor in graph[current_node]:
        if neighbor in visited:  # 如果邻居节点已被访问则跳过
            continue
        dfs(graph, neighbor, visited)
    return visited

# 示例图的定义
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

# 使用DFS算法
![](https://wy-static.wenxiaobai.com/chat-rag-image/4757066815873271879)

start_node = 'A'
visited = dfs(graph, start_node, [])
print(f"Visit order: {visited}")

寻找在上图中A->E的最短路径：

from collections import deque

def dfs(graph, current_node, goal, path, shortest_path, distance):
    path.append(current_node)
    
    if current_node == goal:
        if len(path)-1<distance:
            shortest_path[:] = path
            distance = len(shortest_path)-1
        path.pop()
        return shortest_path, distance
    
    # 遍历当前节点的所有邻居节点
    for neighbor in graph[current_node]:
        if neighbor in path:  # 如果邻居节点已被访问则跳过
            continue
        shortest_path, distance = dfs(graph, neighbor, goal, path, shortest_path, distance)
    
    path.pop()
    return shortest_path, distance

# 示例图的定义
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

# 使用DFS算法
start_node = 'A'
goal = 'F'
path = []
distance = float('inf')
shortest_path, distance = dfs(graph, start_node, goal, path, [], distance)
print("Distance: ",distance)
print(f"Short path: {shortest_path}")

输出结果：

虽然DFS可以找到最短路径，但是需要找到所有的路径之后才能知道最短路径，所有非常耗时，例如在上述BFS中的栅格地图中寻找起点到终点的最短路径是非常困难的，尽管也可以找到最短路径但是非常耗时，所以一般不会使用DFS寻找最短路径。