基于线性回归根据饮食习惯和身体状况估计肥胖水平

基于线性回归根据饮食习惯和身体状况估计肥胖水平

引用

CSDN

1.

https://blog.csdn.net/m0_37758063/article/details/139419413

本文介绍了一个基于线性回归的肥胖水平预测实验。实验使用了一个包含17个特征变量的饮食习惯与身体状况数据集，通过数据预处理、特征分析和模型训练等步骤，最终实现了对个体肥胖水平的预测。实验结果表明，模型具有较高的预测精度，均方误差为0.6537，R^2分数为0.83。

饮食习惯与身体状况数据集介绍

该数据集来自于UCL机器学习知识库，数据集包括墨西哥、秘鲁和哥伦比亚等国基于饮食习惯和身体状况的个体肥胖水平估计数据。数据包含17个属性和2111条记录，这些记录标有类变量肥胖等级，允许使用体重不足、正常体重、超重一级、超重二级、肥胖一级、肥胖二级和肥胖三级的值对数据进行分类。77%的数据是使用Weka工具和SMOTE过滤器综合生成的，23%的数据是通过网络平台直接从用户那里收集的。

Gender、Age、Family_history_with_overweight、FAVC、FCVC、NCP、CAEC、SMOKE、CH2O、CALC、SCC、FAF、TUE作为目标特征，Height、Weight作为体重指数（MBI）的特征，NObeyesdad作为标签，为了确定肥胖水平，使用世界卫生组织提供的表对基于体重指数分析的数据进行了正确分类，如表1所示，得出每个个体的肥胖等级。

体重指数（MBI）计算公式：

实验步骤

3.1 数据分析

首先导入数据集，对数据进行分析。

# 加载数据
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# 查看前五条数据
data = pd.read_csv('dataset.csv')
data.head()

根据程序输出结果，查看数据集数据样本总数和特征变量个数；以及通过数据集前5条数据，查看17个特征变量数据情况。

然后，检查每列缺失值数量。

# 检查每一列缺失值数量
data.isnull().sum()

3.2 可视化处理数据

绘制直方图（共17张），并将异常数据进行剔除。

对自变量进行特征分析，并绘制散点图（共17张）。

绘制热力图，可视化DataFrame中各列之间的相关性。

3.3 导入线性回归模型进行训练

接着通过上述直方图、散点图和热力图分析，对异常数据进行处理，完成数据的预处理，最后通过导入线性回归模型搭建饮食习惯与身体状况预测模型。

# 训练线性回归模型
LR1 = LinearRegression()
LR1.fit(X, y)
# 预测值
y_predict_1 = LR1.predict(X)
# 模型评估
mean_squared_error_1 = mean_squared_error(y, y_predict_1)
r2_score_1 = r2_score(y, y_predict_1)
print("Mean Squared Error:", mean_squared_error_1)
print("R^2 Score:", r2_score_1)

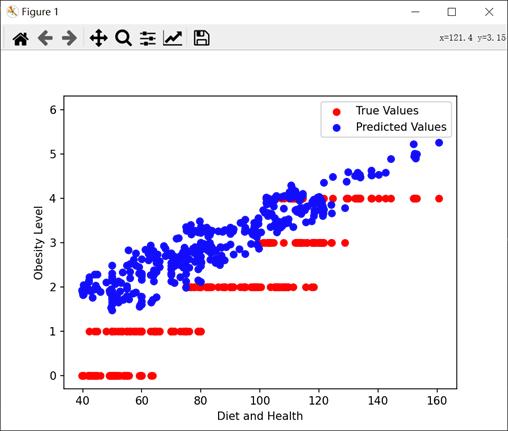
3.4 预测结果

由结果图可以看出，均方误差（MSE）为 0.6537，R2 分数为 0.83。这表明模型的预测效果相对较好，R^2 分数接近于 1，说明模型能够较好地拟合数据，并且均方误差较小，表示模型的预测值与真实值之间的误差较小。

3.5 数据可视化完整代码

![](https://wy-static.wenxiaobai.com/chat-rag-image/80948924723712463)

# 加载数据
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# 查看前五条数据
data = pd.read_csv('dataset.csv')
data.head()
# 检查每一列缺失值数量
data.isnull().sum()
plt.rcParams['font.family'] = ['sans-serif']    #显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
 
fig,ax = plt.subplots(figsize=(6,3), dpi=120)
plt.hist(x = data.Age, # 指定绘图数据
         bins = 15, # 指定直方图中条块的个数
         color = 'skyblue', # 指定直方图的填充色
          edgecolor = 'black' # 指定直方图的边框色
          )
# 添加x轴和y轴标签
plt.xlabel('Age')
plt.ylabel('频数')
# 添加标题
plt.title('年龄分布')
plt.title('年龄分布')
#%%
plt.rcParams['font.family'] = ['sans-serif']    #显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
 
fig,ax = plt.subplots(figsize=(6,3), dpi=120)
plt.hist(x = data.Height, # 指定绘图数据
         bins = 15, # 指定直方图中条块的个数
         color = 'skyblue', # 指定直方图的填充色
          edgecolor = 'black' # 指定直方图的边框色
          )
# 添加x轴和y轴标签
plt.xlabel('Height')
plt.ylabel('频数')
# 添加标题
plt.title('身高分布')
plt.title('身高分布')
#%%
%matplotlib inline
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(10,10))
fig1 =plt.subplot(231)
plt.scatter(data.loc[:,'Weight'],data.loc[:,'NObeyesdad'])
plt.title('Weight VS Obesity')
%matplotlib inline
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(10,10))
fig1 =plt.subplot(231)
plt.scatter(data.loc[:,'Age'],data.loc[:,'NObeyesdad'])
plt.title('Age VS Obesity')
import seaborn as sns
plt.figure(figsize=(24,16))
ax = sns.heatmap(data.corr(), square=True, annot=True, fmt='.2f')
ax.set_xticklabels(ax.get_xticklabels(), rotation=90)  
bottom, top = ax.get_ylim()
ax.set_ylim(bottom + 0.5, top - 0.5)  

4. 完整代码(模型训练与评估)

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns
# 加载数据
data = pd.read_csv('dataset.csv')
v_bos = pd.DataFrame(data)  # 查看波士顿数据集前5条数据，查看这13个变量数据情况
print(v_bos.head(5))
# 选择特征变量和目标变量
X = data[['Weight']]  # 特征变量，选择 'Weight' 列作为输入变量
y = data['NObeyesdad']  # 目标变量，选择 'NObeyesdad' 列作为目标变量
# 将目标变量转换为数值型，使用 Label Encoding
class_mapping = {
    'Insufficient_Weight': 0,
    'Normal_Weight': 1,
    'Overweight_Level_I': 2,
    'Overweight_Level_II': 3,
    'Obesity_Type_I': 4,
    'Obesity_Type_II': 5,
    'Obesity_Type_III': 6
}
y = y.map(class_mapping)
X = np.array(X).reshape(-1, 1)
# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 训练线性回归模型
LR1 = LinearRegression()
LR1.fit(X_train, y_train)
# 在测试集上进行预测
y_predict_1 = LR1.predict(X_test)
# 模型评估
mean_squared_error_1 = mean_squared_error(y_test, y_predict_1)
r2_score_1 = r2_score(y_test, y_predict_1)
print("Mean Squared Error:", mean_squared_error_1)
print("R^2 Score:", r2_score_1)
# 绘制真实值和预测值的对比图
fig = plt.figure(figsize=(8, 5))
plt.scatter(X_test, y_test, label='True Values')
plt.plot(X_test, y_predict_1, color='red', label='Predicted Values')
plt.xlabel('Weight')  # 横坐标标签
plt.ylabel('NObeyesdad')  # 纵坐标标签
plt.legend()
plt.show()

参考文献

[1]饮食习惯与身体状况数据集