动态规划算法详解：原理、实现及应用场景

动态规划算法详解：原理、实现及应用场景

引用

CSDN

1.

https://blog.csdn.net/wnm23/article/details/140801947

动态规划（Dynamic Programming，DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学等领域中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。本文将详细介绍动态规划的基本概念、算法原理、数据结构、使用场景、算法实现以及与其他算法的对比等。

一、引言

动态规划（Dynamic Programming，DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学等领域中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划算法的核心思想是将复杂问题分解为更小的子问题，并利用这些子问题的解来构造原问题的解。

二、算法原理

动态规划算法的核心思想是分治法，将原问题分解为相对简单的子问题，递归地求解子问题，然后合并子问题的解以得到原问题的解。动态规划通常用于求解最优化问题，如求解单源最短路径、最大子序列和、最小路径覆盖等。动态规划算法的基本步骤如下：

• 定义状态：确定原问题的最优解与哪些子问题的解相关。
• 确定状态转移方程：找出原问题的最优解如何通过子问题的解来表达。
• 计算顺序：确定计算子问题解的顺序，确保在求解任一子问题时，其所有子问题的解已经计算完毕。
• 避免重复计算：利用数组或哈希表存储已经计算过的子问题的解，避免重复计算。

三、数据结构

动态规划算法主要涉及以下数据结构、通常使用以下数据结构来存储子问题的解：

• 数组：用于存储一维或二维状态。
• 哈希表：用于存储不规则的状态，以便快速查找。
• 矩阵：用于存储多维状态。

四、使用场景

动态规划算法适用于以下场景：

• 最优化问题：如单源最短路径、最大子序列和、最小路径覆盖等。
• 字符串匹配：如KMP算法。
• 背包问题：如0-1背包问题、完全背包问题等。
• 序列比对：如最长公共子序列（LCS）和最长递增子序列（LIS）。
• 股票买卖问题：如最大利润问题。
• 文本编辑距离：如 Levenshtein 距离。

五、算法实现

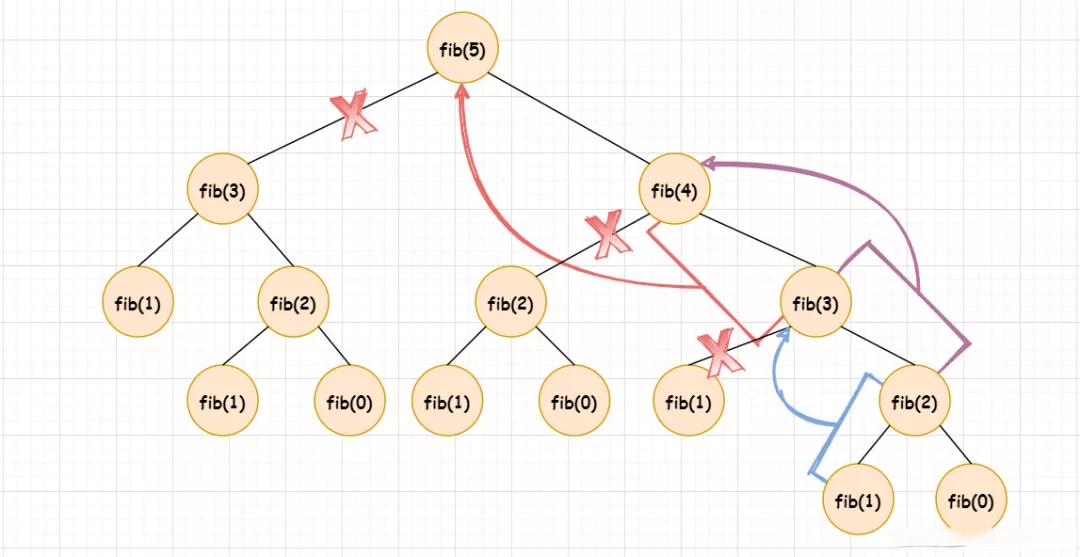
动态规划算法的一个简单示例，用于求解斐波那契数列：

• F(0) = 0
• F(1) = 1
• F(n) = F(n-1) + F(n-2) (n ≥ 2)

function fibonacci(n):
    if n <= 1:
        return n
    
    # 创建一个数组来存储子问题的解
    fib = [0] * (n + 1)
    fib[0] = 0
    fib[1] = 1
    # 计算子问题的解，并存储在数组中
    for i from 2 to n:
        fib[i] = fib[i - 1] + fib[i - 2]
    return fib[n]
  

六、其他同类算法对比

• 贪心算法：与动态规划类似，但只考虑当前状态下的最优解，不考虑全局最优解。
  
• 回溯算法：通过尝试所有可能的解，找到问题的解，但效率较低。
  特性 动态规划 贪心算法 回溯算法
  适用场景 最优解问题 局部最优解 组合问题
  解决方式 存储子问题结果 逐步选择局部最优解 尝试所有可能
  时间复杂度 O(n) 或 O(n^2) O(n log n) 或 O(n) O(2^n) 或 O(n!)
  空间复杂度 O(n) 或 O(n^2) O(1) O(n)

七、多语言实现

以下是动态规划算法的简化版实现：

Java

public class DynamicProgramming {
    public static int fibonacci(int n) {
        if (n <= 1) {
            return n;
        }
        int[] fib = new int[n + 1];
        fib[0] = 0;
        fib[1] = 1;
        for (int i = 2; i <= n; i++) {
            fib[i] = fib[i - 1] + fib[i - 2];
        }
        return fib[n];
    }
}
  

Python

def fibonacci(n):
    if n <= 1:
        return n
    fib = [0] * (n + 1)
    fib[0] = 0
    fib[1] = 1
    for i in range(2, n + 1):
        fib[i] = fib[i - 1] + fib[i - 2]
    return fib[n]
  

C++

#include <vector>
using namespace std;
int knapsack(int W, vector<int>& wt, vector<int>& val, int n) {
    vector<vector<int>> K(n+1, vector<int>(W+1, 0));
    for (int i = 0; i <= n; i++) {
        for (int w = 0; w <= W; w++) {
            if (i == 0 || w == 0)
                K[i][w] = 0;
            else if (wt[i-1] <= w)
                K[i][w] = max(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w]);
            else
                K[i][w] = K[i-1][w];
        }
    }
    return K[n][W];
}  

Go

package main
import (
    "fmt"
)
func knapsack(W int, wt []int, val []int, n int) int {
    K := make([][]int, n+1)
    for i := range K {
        K[i] = make([]int, W+1)
    }
    for i := 0; i <= n; i++ {
        for w := 0; w <= W; w++ {
            if i == 0 || w == 0 {
                K[i][w] = 0
            } else if wt[i-1] <= w {
                K[i][w] = max(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w])
            } else {
                K[i][w] = K[i-1][w];
            }
        }
    }
    return K[n][W];
}
func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}
func main() {
    fmt.Println(knapsack(50, []int{10, 20, 30}, []int{60, 100, 120}, 3))
}  

八、实际服务应用场景代码框架

假设我们有一个实际的服务应用场景，我们需要计算一个序列中所有元素的和，其中每个元素是一个整数。以下是使用动态规划算法来实现这个功能的代码框架：

def sum_sequence(sequence):
    if not sequence:
        return 0
    # 创建一个数组来存储子问题的解
    dp = [0] * (len(sequence) + 1)
![](https://wy-static.wenxiaobai.com/chat-rag-image/4390631227828152247)
    dp[0] = 0
    # 计算子问题的解，并存储在数组中
    for i in range(1, len(sequence) + 1):
        dp[i] = dp[i-1] + sequence[i-1]
    return dp[-1]
# 示例使用
sequence = [1, 2, 3, 4, 5]
print(sum_sequence(sequence))  

import java.util.*;
public class Knapsack {
    public static int knapsack(int[] weights, int[] values, int capacity) {
        int n = weights.length;
        int[][] dp = new int[n + 1][capacity + 1];
        for (int i = 1; i <= n; i++) {
            for (int w = 0; w <= capacity; w++) {
                if (weights[i - 1] <= w) {
                    dp[i][w] = Math.max(dp[i - 1][w], dp[i - 1][w - weights[i - 1]] + values[i - 1]);
                } else {
                    dp[i][w] = dp[i - 1][w];
                }
            }
        }
        return dp[n][capacity];
    }
    public static void main(String[] args) {
        int[] weights = {2, 3, 4, 5};
        int[] values = {3, 4, 5, 6};
        int capacity = 5;
        System.out.println("Maximum value in Knapsack = " + knapsack(weights, values, capacity));
    }
}