递归求解二叉树问题代码及图解(104、111、112、129、1448)
递归求解二叉树问题代码及图解(104、111、112、129、1448)
递归是解决二叉树问题的一种常用方法,本文将通过5个具体的二叉树问题,详细讲解递归算法的实现过程。这些问题包括:二叉树的最大深度、最小深度、路径总和、根节点到叶节点数字之和以及统计好节点的数目。每个问题都包含了详细的代码实现和复杂度分析,帮助读者深入理解递归在二叉树问题中的应用。
104. 二叉树的最大深度
给定一个二叉树 root,返回其最大深度。二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
提示:
- 树中节点的数量在
[0, 104]区间内。 -100 <= Node.val <= 100
代码
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if root == None:
return 0
lDeep = self.maxDepth(root.left)
rDeep = self.maxDepth(root.right)
maxD = max(lDeep, rDeep) + 1
return maxD
图解
不关注细节,只看大轮廓或者最后一步
重点在归:
复杂度
时间复杂度:O(n),其中 n 为二叉树节点的个数。
空间复杂度:O(height),其中 height 表示二叉树的高度。
111. 二叉树的最小深度
给定一个二叉树 root,返回其最小深度。二叉树的最小深度是指从根节点到最近叶子节点的最短路径上的节点数。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
提示:
- 树中节点的数量在
[0, 104]区间内。 -100 <= Node.val <= 100
代码
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
if not root :
return 0
if not root.right:
return self.minDepth(root.left) + 1
if not root.left:
return self.minDepth(root.right) + 1
minD = min(self.minDepth(root.left), self.minDepth(root.right)) + 1
return minD
图解
重点在归:
复杂度
时间复杂度:O(n),其中 n 为二叉树节点的个数。
空间复杂度:O(height),其中 height 表示二叉树的高度。
112. 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum。判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和 targetSum。如果存在,返回 true;否则,返回 false。
叶子节点是指没有子节点的节点。
示例 1:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。
提示:
- 树中节点的数目在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
代码
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
self.flag = False
self.targetSum = targetSum
def dfs(node:Optional[TreeNode], mySum:int):
if node == None:
return
mySum += node.val
if node.left == None and node.right == None and mySum == self.targetSum:
self.flag = True
dfs(node.left,mySum)
dfs(node.right,mySum)
dfs(root,0)
return self.flag
图解
重点在递:
复杂度
时间复杂度:O(n),其中 n 为二叉树节点的个数。
空间复杂度:O(height),其中 height 表示二叉树的高度。
129. 求根节点到叶节点数字之和
给你一个二叉树的根节点 root,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径
1 -> 2 -> 3表示数字123。
计算从根节点到叶节点生成的所有数字之和。
叶节点是指没有子节点的节点。
示例 1:
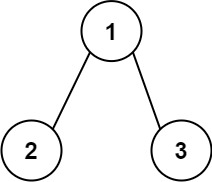
输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
示例 2:
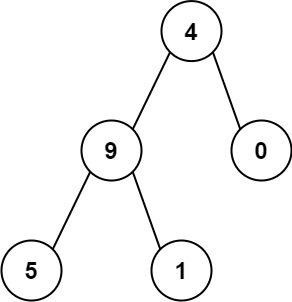
输入:root = [4,9,0,5,1]
输出:1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此,数字总和 = 495 + 491 + 40 = 1026
提示:
- 树中节点的数目在范围
[1, 1000]内 0 <= Node.val <= 9- 树的深度不超过
10
代码
class Solution:
def sumNumbers(self, root: Optional[TreeNode]) -> int:
self.Sum = 0
def dfs(node:Optional[TreeNode],c_sum):
if node == None:
return
c_sum = c_sum*10 + node.val
if node.left is None and node.right is None:
self.Sum += c_sum
dfs(node.left,c_sum)
dfs(node.right,c_sum)
return
dfs(root,0)
return self.Sum
图解
重点在递:
复杂度
时间复杂度:O(n),其中 n 为二叉树节点的个数。
空间复杂度:O(height),其中 height 表示二叉树的高度。
1448. 统计二叉树中好节点的数目
给你一棵根为 root 的二叉树,请你返回二叉树中好节点的数目。
「好节点」X 定义为:从根到该节点 X 所经过的节点中,没有任何节点的值大于 X 的值。
示例 1:
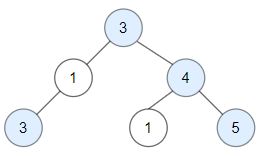
输入:root = [3,1,4,3,null,1,5]
输出:4
解释:图中蓝色节点为好节点。
根节点 (3) 永远是个好节点。
节点 4 -> (3,4) 是路径中的最大值。
节点 5 -> (3,4,5) 是路径中的最大值。
节点 3 -> (3,1,3) 是路径中的最大值。
示例 2:
输入:root = [3,3,null,4,2]
输出:3
解释:节点 2 -> (3, 3, 2) 不是好节点,因为 "3" 比它大。
示例 3:
输入:root = [1]
输出:1
解释:根节点是好节点。
提示:
- 二叉树中节点数目范围是
[1, 10^5]。 - 每个节点权值的范围是
[-10^4, 10^4]。
代码
class Solution:
def goodNodes(self, root: Optional[TreeNode]) -> int:
self.ans = 0
def dfs(node:Optional[TreeNode],MAX:int):
if node == None:
return
MAX = max(MAX,node.val)
if MAX == node.val:
self.ans += 1
dfs(node.left,MAX)
dfs(node.right,MAX)
return
dfs(root,-sys.maxsize - 1)
return self.ans
图解
重点在递
复杂度
时间复杂度:O(n),其中 n 为二叉树节点的个数。
空间复杂度:O(height),其中 height 表示二叉树的高度。