详解Lasso回归：原理、代码实现与应用场景

详解Lasso回归：原理、代码实现与应用场景

引用

CSDN

1.

https://blog.csdn.net/qq_65664454/article/details/145395583

Lasso回归是一种常用的机器学习算法，通过在损失函数中引入L1正则化项，可以实现特征选择和模型简化。本文将详细介绍Lasso回归的基本原理、数学推导、代码实现以及应用场景，帮助读者深入理解这一算法的核心思想和实际应用。

系列文章目录

第一章：Pyhton机器学习算法之KNN
第二章：Pyhton机器学习算法之K—Means
第三章：Pyhton机器学习算法之随机森林
第四章：Pyhton机器学习算法之线性回归
第五章：Pyhton机器学习算法之有监督学习与无监督学习
第六章：Pyhton机器学习算法之朴素贝叶斯
第七章：Pyhton机器学习算法之XGBoost
第八章：Pyhton机器学习算法之GBDT
第九章：Pyhton机器学习算法之岭回归
第十章：Pyhton机器学习算法之lasso回归

目录
系列文章目录
前言
一、基本原理：
二、基本模型：
三、数学原理：
四、正则项选择：
五、模型评估：
六、代码实战：
七、优缺点：
八、应用场景：
总结

前言

Lasso回归通过在损失函数中引入L1正则化项，鼓励模型将一些不重要的特征系数缩减为零，从而实现特征选择的效果。通过Lasso回归，可以从高维特征中筛选出关键特征，得到更加精简且有效的模型。这在领域如基因表达数据分析、金融数据建模等高维数据场景中非常有用。

一、基本原理：

Lasso回归在普通最小二乘法的基础上增加一个正则惩罚项L1，用于约束模型中的系数，使某些系数变为零，从而实现特征选择。Lasso算法生成的模型是稀疏的，即模型中只有少数几个非零系数，这有助于提高模型的可解释性。

二、基本模型：

• 其中，
  是普通的线性回归目标项；
• 是Lasso回归的惩罚项，其中λ 是一个调整惩罚程度的参数
  简单来说，lasso回归在拟合数据时，不仅考虑了预测误差（即预测值与实际值之间的差距），还考虑了回归系数的大小。通过引入正则化项，lasso回归会使得较小回归系数变为零，从而达到特征选择的目的，减少模型的复杂度和过拟合的风险。

三、数学原理：

普通最小二乘法（OLS）：
最小化残差平方和：
Lasso回归：
在OLS的基础上，加上一个L1 正则化项：
其中，
是正则化项，它通过增加非零系数的数量来惩罚模型的复杂性。
梯度下降法：
为了最小化这个目标函数，我们可以使用梯度下降法。梯度下降的更新规则如下：
其中，α 是学习率，
是目标函数的梯度
计算梯度时，普通最小二乘项的梯度是：
正则化项的梯度稍微复杂一些，因为 L1范数的导数在零点不连续。其导数形式是：
其中，
表示符号函数。
综上，Lasso回归的梯度：
注意：梯度下降法仅是解决这个优化问题的一种方法，也有其他方法如坐标下降法
通过迭代梯度下降，直至收敛或者到最大迭代次数

四、正则项选择：

• 通常通过交叉验证（Cross-Validation）的方法选择最优的正则化参数 λ。具体步骤包括：
• 将数据集划分为训练集和验证集。
• 对一系列不同的 λ值训练lasso回归模型。
• 在验证集上评估模型性能，选择使模型在验证集上表现最好的 λ。

五、模型评估：

使用计算得到的回归系数 β，在训练集和测试集上评估模型的性能。常用的评估指标包括均方误差（MSE）、R平方值等。

六、代码实战：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import GridSearchCV

# 加载数据
from sklearn.datasets import fetch_california_housing
data = fetch_california_housing()
df = pd.DataFrame(data.data,columns=data.feature_names)
df['MedHouseVal'] = data.target

# 分离特征和目标变量
X = df.drop('MedHouseVal', axis=1)
y = df['MedHouseVal']

# 数据分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 特征缩放
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

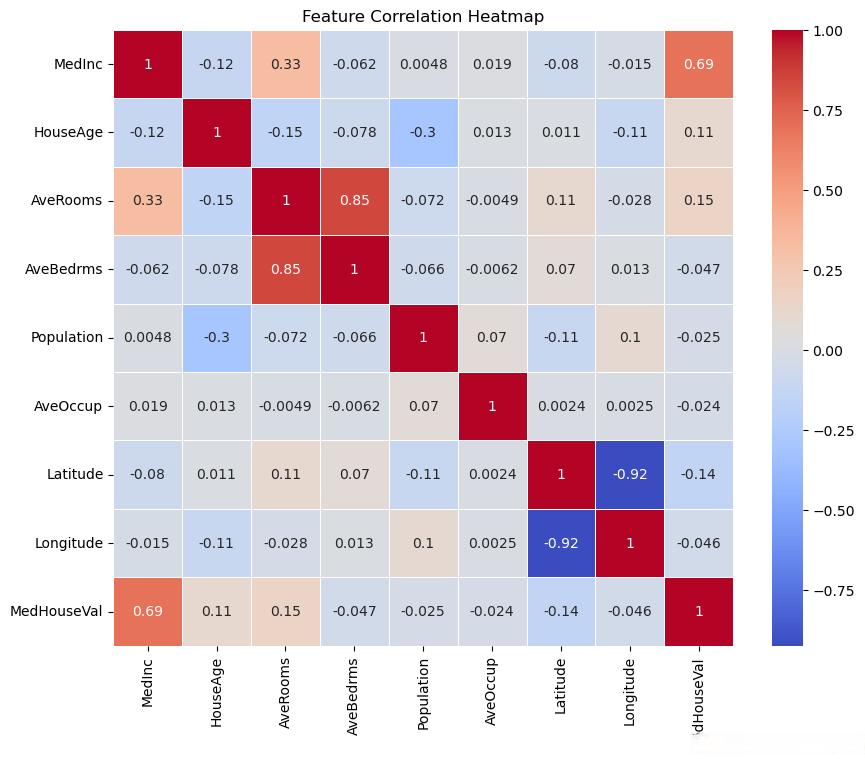
# 特征相关性
plt.figure(figsize=(10,8))
sns.heatmap(df.corr(),annot=True,cmap='coolwarm',linewidths=0.5)
plt.title('Feature Correlation Heatmap')
plt.show()  

效果如下：

优化lasso模型：

# 建立 Lasso 模型
lasso=Lasso()
# 定义超参数网格
param_grid={'alpha':np.logspace(-4,4,50)}
![](https://wy-static.wenxiaobai.com/chat-rag-image/14851649955762191488)
# 网格搜索
grid_search=GridSearchCV(lasso,param_grid,cv=5,scoring='neg_mean_squared_error')
grid_search.fit(X_train_scaled,y_train)
# 最佳超参数
best_alpha=grid_search.best_params_['alpha']
print(f'Best alpha: {best_alpha}')
# 训练最终模型
lasso_opt=Lasso(alpha=best_alpha)
lasso_opt.fit(X_train_scaled,y_train)  

模型评估：

# 预测
y_pred_train=lasso_opt.predict(X_train_scaled)
y_pred_test=lasso_opt.predict(X_test_scaled)
# 评估
mse_train=mean_squared_error(y_train,y_pred_train)
mse_test=mean_squared_error(y_test,y_pred_test)
r2_train=r2_score(y_train,y_pred_train)
r2_test=r2_score(y_test,y_pred_test)
print(f'MSE (Train):{mse_train}')
print(f'MSE (Test):{mse_test}')
print(f'R^2 (Train):{r2_train}')
print(f'R^2 (Test):{r2_test}')
# 可视化
plt.figure(figsize=(10,6))
plt.scatter(y_test,y_pred_test,alpha=0.6,color='b')
plt.plot([0,5],[0,5],'r--')
plt.xlabel('Actual')
plt.ylabel('Predicted')
plt.title('Actual vs Predicted House Prices')
plt.show()  

效果如下：

注：确保所有特征进行标准化，避免特征值差异过大对模型的影响

七、优缺点：

优点：

1. 特征选择：Lasso回归会将一些不重要的特征的系数缩减为零，从而实现特征选择。这使得模型更加简洁和易于解释。
2. 减少过拟合：通过引入正则化项，Lasso回归可以有效地减少过拟合，提高模型的泛化能力。
3. 简单高效：Lasso回归相对简单，计算效率高，适用于处理高维数据。

缺点

1. 多重共线性问题：当特征之间存在多重共线性时，Lasso回归可能无法正确选择特征，导致模型性能下降。
2. 计算复杂度：在大规模数据集上，Lasso回归的计算复杂度可能较高，尤其是当使用网格搜索优化超参数时。
3. 
   模型解释性：虽然Lasso回归能进行特征选择，但对结果的解释性仍可能受到数据特性的影响，有时难以完全理解模型的行为。

八、应用场景：

1. 经济学领域：

• 在预测经济增长因素时，Lasso回归可以帮助经济学家从众多潜在的变量（如通货膨胀率、失业率、利率等）中筛选出对经济增长有显著影响的变量，从而构建更简洁有效的经济增长模型。

2. 医学研究：

• Lasso回归在研究疾病的风险因素时非常有用。例如，在研究心血管疾病与年龄、血压、血脂、生活习惯等多种因素之间的关系时，Lasso回归可以筛选出关键的风险因素，为疾病的预防和治疗提供依据。
• 在临床数据建模中，Lasso回归也常用于筛选生物标志物和构建临床预测模型。通过Lasso回归，可以从大量的临床数据中筛选出对疾病诊断或预测最重要的一些指标，从而提高模型的准确性和实用性。

3. 金融领域：

• Lasso回归在金融领域的应用主要体现在挖掘基金重仓股和股票预测等方面。通过给定的基金历史表现数据和市场其他股票的表现数据，Lasso回归可以找出对基金收益影响最大的那些股票，为投资者提供重要的参考信息。
• 此外，Lasso回归还可以用于信用评分模型的构建，通过筛选对信用评分有显著影响的变量，提高模型的预测能力和稳定性。

4. 计算机视觉：

• 在计算机视觉领域，Lasso回归主要应用于目标检测和物体识别。通过Lasso回归进行特征选择，可以减少特征extractor和分类器的复杂性，从而提高目标检测模型和物体识别模型的泛化能力。
• 具体来说，Lasso回归可以用于学习特征extractor（将图像转换为特征向量的函数）和分类器（将特征向量映射到类别标签的函数），通过筛选出的关键特征来提高模型的准确性和效率。

5. 其他领域：

• Lasso回归还广泛应用于市场营销、生态学、生物学等多个领域。例如，在市场营销中，Lasso回归可以用于筛选对销售额或市场份额有显著影响的营销因素；在生态学中，Lasso回归可以用于研究物种多样性与生态因子之间的关系；在生物学中，Lasso回归可以用于筛选与基因表达或疾病发生相关的基因等。

总结

综上所述，Lasso回归作为一种先进的回归分析技术，在特征选择、处理共线性问题以及提高模型泛化能力等方面展现出显著优势。通过合理的模型选择和调优，Lasso回归能够在多个领域发挥重要作用，为数据分析和预测提供有力支持。