基于MATLAB的信号频谱分析和参数优化、FFT、窗函数的使用

基于MATLAB的信号频谱分析和参数优化、FFT、窗函数的使用

引用

CSDN

1.

https://blog.csdn.net/weixin_74392201/article/details/144095902

本文将通过一个具体的信号处理案例，详细介绍如何使用MATLAB进行信号频谱分析。文章将从任务目标、任务分析、MATLAB程序实现等多个维度展开，重点讲解FFT函数的使用、参数优化以及窗函数的应用。

任务目标

对模拟信号 (x(t) = 0.1 \sin(2\pi f_0t) + 2 \sin(2\pi f_1t)) 进行采样，其中 (f_0 = 100Hz)，(f_1 = 110Hz)，采样率为 (1000Hz)。在MATLAB中用FFT进行频谱分析。

任务分析

1. 采样率：采样率约为信号频率的10倍，满足采样定理。
2. 采样长度：采样长度要满足 (N > f_s / \Delta f = 1000 / (110 - 100) = 100)，才能保证FFT频谱精度小于10Hz，进而区分出两个频率。取采样点数 (N = 128)，采样时间 (t = N / f_s = 128 / 1000 = 128ms)。
3. 信号幅度问题：由于两个频率接近，且其中一个幅值超过另外一个的10倍，此时极容易发生峰值混叠现象。解决方法是延长采样时间和加窗函数。

MATLAB程序及结果

1. 原始程序

clear; clc; close all;
%% 参数配置
f0 = 100;    % 100 Hz
f1 = 110;    % 110 Hz
fs = 1000;   % 采样率 1000 Hz
N = 128;     % 采样点数（实际信号长度）
N_FFT = 128 ;% FFT点数（通常选择2的幂次，大于或等于信号长度）
% 生成时间向量
t = (0:N-1)/fs;
% 生成信号
x = 0.1 * sin(2 * pi * f0 * t) + 2 * sin(2 * pi * f1 * t);
% 不加窗
x_windowed = x;
% 计算FFT
X = fft(x_windowed, N_FFT);
% 计算频率向量
f = (0:N_FFT-1)*(fs/N_FFT);
% 计算双边频谱的幅度并转换为单边频谱
X_mag = abs(X/N_FFT);
X_mag_single_side = X_mag(1:N_FFT/2+1); % 包含DC分量，且已经是单边频谱的正确幅度
% 绘制频谱图
figure;
stem(f(1:N_FFT/2+1), X_mag_single_side);
title('单边频谱分析');
xlabel('频率 (Hz)');
ylabel('幅度');
grid on;
xlim([0 fs/2]);

2. 参数优化

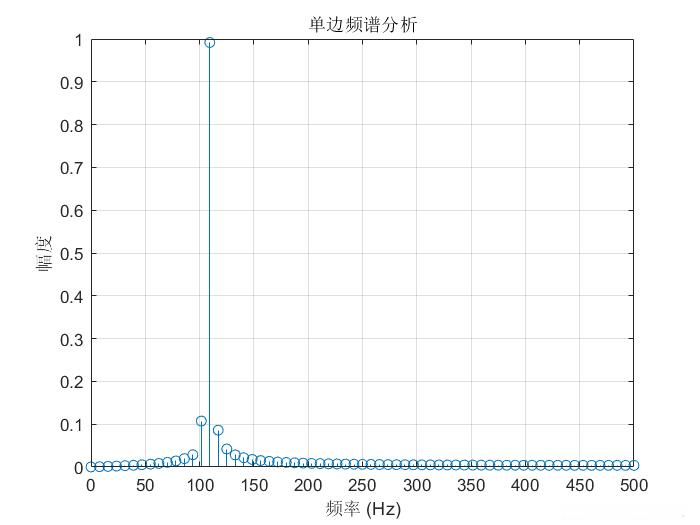
可以看到100Hz分量被淹没。此时由于频谱分量过于接近，需要提高采样时间来进一步增大FFT频谱分辨率。我们将采样点数N提高至1000，此时采样时间为1秒。FFT点数设置为1024。再次运行。

观察到频谱中出现周期性的半波，这是Sa函数的副瓣，是因为使用了矩形窗截断导致了频谱泄露，110Hz频率分量泄露后淹没了100Hz的频率分量。

所以我们要对信号进行加窗，使用旁瓣更小的窗函数来突出100Hz分量。

% 选择窗函数（这里以汉宁窗为例）
window = hanning(N);
![](https://wy-static.wenxiaobai.com/chat-rag-image/1338129705755549916)
% 将信号与窗函数相乘
x_windowed = x .* window'; % 注意：window' 是为了确保维度匹配，但在这个例子中不是必需的，因为x和window都是列向量
![](https://wy-static.wenxiaobai.com/chat-rag-image/10244873105976494915)

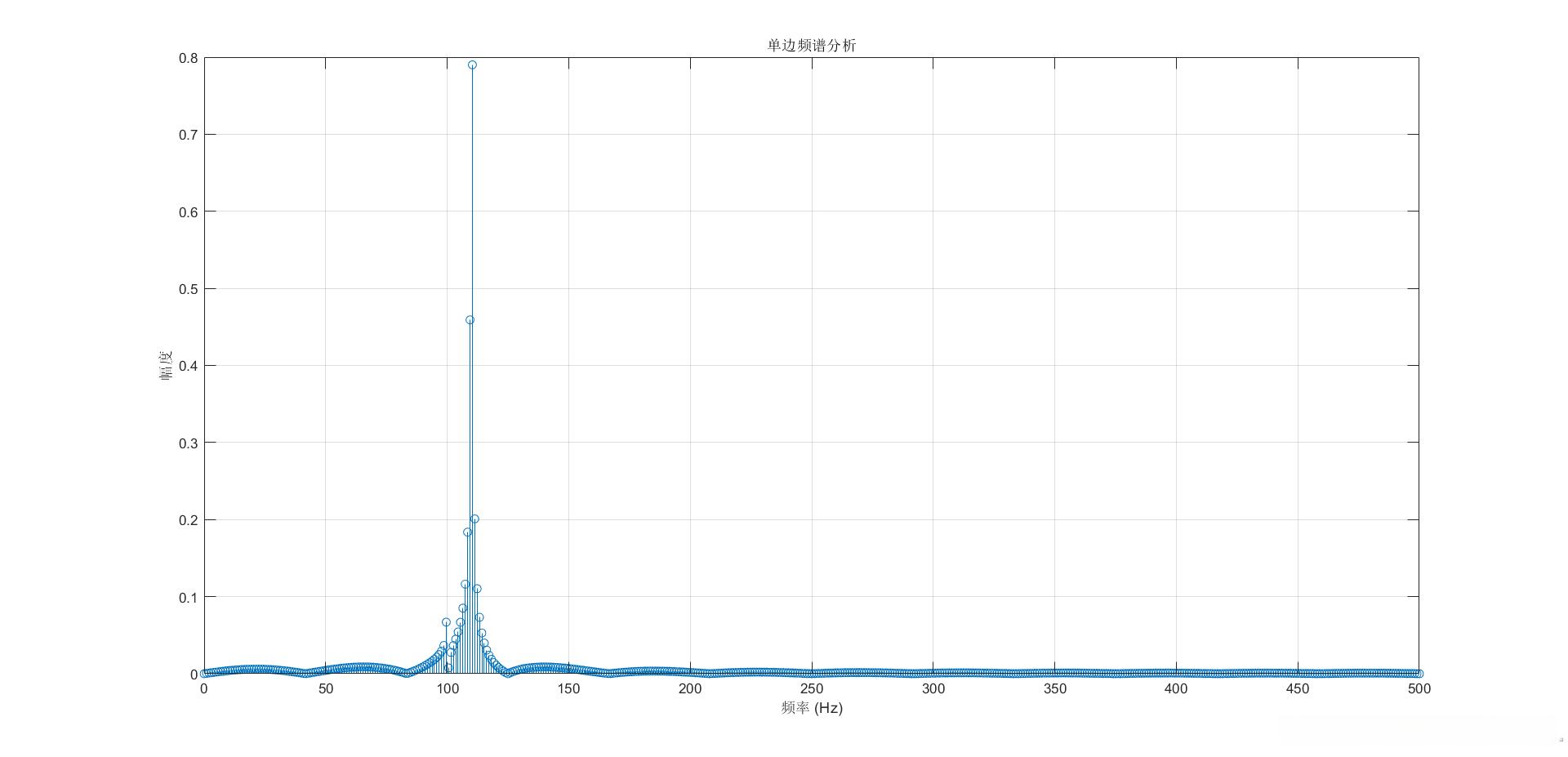
运行结果如下图所示。

可以看到，频谱泄露现象大大减轻了。

3. 验证

我们测量100Hz和110Hz频率分量的幅值。

发现幅度比值与原始信号幅度比值差别不大，相对误差为 (0.5 / 20 * 100% = 2.5%)。