机器学习：从贝叶斯定理到朴素贝叶斯分类器的应用

机器学习：从贝叶斯定理到朴素贝叶斯分类器的应用

引用

CSDN

1.

https://blog.csdn.net/m0_65065095/article/details/146206806

前言

分类算法常用的有很多种，朴素贝叶斯算法是其中一个比较常用的，之所以称为朴素贝叶斯算法主要是因为该算法最基本的原理是基于贝叶斯定理的，称为朴素是因为该算法成立的前提是特征之间必须得是独立的。
朴素贝叶斯（Naive Bayes）算法理论基础是基于贝叶斯定理和条件独立性假设的一种分类方法。

一、贝叶斯定理

公式如下：

通俗地说在 B 出现的前提下 A 出现的概率，等于 A 和 B 都出现的概率除以 B 出现的概率。

二、朴素贝叶斯分类器

“朴素贝叶斯”（Naive Bayes）既可以是一种算法——朴素贝叶斯算法，也可以是一种模型——朴素贝叶斯分类模型（分类器）。
数学公式可以写为：

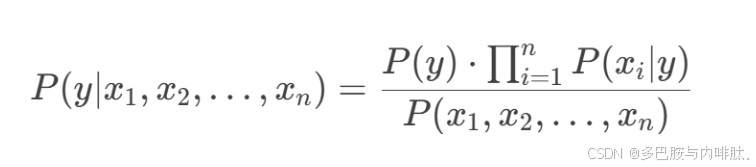
y为类别变量；

x1，x2，x3,…,xn为特征变量。

三、代码实现

数学公式我们可以求解，然而机器学习所给的是一行一行的数据集，那么贝叶斯是如何将样本数据进行计算实现预测的呢？
这是一个鸢尾花数据集：
接下来我们就用代码实现预测：

1.引入库

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB#导入朴素贝叶斯分类器
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt

2.可视化混淆矩阵

def cm_plot(y,yp):
    cm = confusion_matrix(y, yp)
    plt.matshow(cm, cmap=plt.cm.Blues)
    plt.colorbar()
    for x in range(len(cm)):
        for y in range(len(cm)):
            plt.annotate(cm[x,y],xy=(y,x),horizontalalignment='center',
                         verticalalignment='center')
            plt.ylabel('True label')
            plt.xlabel('Predicted label')
    return plt

3、数据预处理

data = pd.read_csv("iris.csv",header=None)#header=None代表读取的csv文件是没有表头
data = data.drop(0, axis=1)#把第1列删除，

因为第一列是索引没有用，我们把它删掉。

4、切分数据集

X_whole = data.drop(5, axis=1)
y_whole = data[5]
x_train_w, x_test_w, y_train_w, y_test_w = \
    train_test_split(X_whole, y_whole, test_size = 0.2, random_state = 0)

5、创建朴素贝叶斯分类器并进行预测

classifier = MultinomialNB(alpha=1)
classifier.fit(x_train_w, y_train_w)#传入训练集数据
"""训练集预测"""
#绘制训练集混淆矩阵
train_pred = classifier.predict(x_train_w)#自测
cm_plot(y_train_w, train_pred).show()
"""测试集预测"""
test_pred = classifier.predict(x_test_w)
cm_plot(y_test_w, test_pred).show()

四. 贝叶斯算法的优缺点

1.优点

• 简单高效：计算速度快，适合大规模数据集。
• 对小规模数据表现良好：即使在数据较少的情况下也能取得不错的效果。
• 对缺失数据不敏感：能够处理缺失值问题。
• 可解释性强：基于概率的分类结果易于理解

2.缺点

• 独立性假设过强：现实中特征之间往往存在相关性，独立性假设可能导致模型性能下降。
• 对输入数据分布敏感：如果数据分布与假设不符（如非高斯分布），模型性能可能较差。
• 零概率问题：当某个特征值在训练集中未出现时，会导致概率为零，可通过拉普拉斯平滑（Laplace Smoothing）解决。

总结

朴素贝叶斯的算法精度不会太高，因为它更适用于自然语言处理，对数据处理方面效果不是特别好。