C++ 堆结构和堆排序（从顶到底/从底到顶的大顶堆）+ 优化

创作时间:

作者:

@小白创作中心

C++ 堆结构和堆排序（从顶到底/从底到顶的大顶堆）+ 优化

引用

CSDN

https://blog.csdn.net/weixin_41987016/article/details/138362120

堆结构和堆排序是C++编程中重要的数据结构和算法之一。本文将详细介绍堆的插入（heapInsert）和向下调整（heapify）操作，并提供两种建立大根堆的方法：从顶到底和从底到顶。同时，本文还将分析堆排序的时间复杂度，并给出完整的代码实现。

一、堆结构和堆排序

（1）heapInsert，向上调整大根堆和 heapify，向下调整大根堆

// i位置的数，向上调整大根堆
// arr[i] = x，x是新来的！往上看，直到不比父亲大，或者来到0位置(顶)
void heapInsert(vector<int>& arr, int i) {
    // i -> 父: (i - 1) / 2
    while (arr[i] > arr[(i - 1) / 2]) {
        swap(arr, i, (i - 1) / 2);
        i = (i - 1) / 2;
    }
}  

// i位置的数，变小了，又想维持大根堆结构
// 向下调整大根堆
// 当前堆的大小为size
void heapify(vector<int>& arr, int i, int size) {
    int l = i * 2 + 1;
    
    while (l < size) {
        // 有左孩子，l
        // 右孩子，l+1
        // 评选，最强的孩子，是哪个下标的孩子
        int best = l + 1 < size && arr[l + 1] > arr[l] ? l + 1 : l;
        // 上面已经评选了最强的孩子，接下来，当前的数和最强的孩子之前，最强下标是谁
        best = arr[best] > arr[i] ? best : i;
        // 如果最强的下标，是当前的数，那么当前的数已经满足大根堆结构，退出
        if (best == i) { // 最强的是自己
            break;
        }
        swap(arr, best, i);
        i = best;
        l = i * 2 + 1;
    }
}

二、从顶到底建立大根堆

完整代码：

#include <iostream>
using namespace std;
#include <vector>
// 堆结构和堆排序，填函数练习风格
// 测试链接 : https://leetcode.cn/problems/sort-an-array/
class heapSort {
public:
    vector<int> sortArray(vector<int> arr) {
        if (arr.size() > 1) {
            // heapSort1 为从顶到底建堆然后排序
            // heapSort2 为从底到顶建堆然后排序
            // 用哪个都可以
            heapSort1(arr);
            //heapSort2(arr);
        }
        return arr;
    }
    // i位置的数，向上调整大根堆
    // arr[i] = x，x是新来的！往上看，直到不比父亲大，或者来到0位置(顶)
    void heapInsert(vector<int>& arr, int i) {
        // i -> 父: (i - 1) / 2
        while (arr[i] > arr[(i - 1) / 2]) {
            swap(arr, i, (i - 1) / 2);
            i = (i - 1) / 2;
        }
    }
    // i位置的数，变小了，又想维持大根堆结构
    // 向下调整大根堆
    // 当前堆的大小为size
    void heapify(vector<int>& arr, int i, int size) {
        int l = i * 2 + 1;
        
        while (l < size) {
            // 有左孩子，l
            // 右孩子，l+1
            // 评选，最强的孩子，是哪个下标的孩子
            int best = l + 1 < size && arr[l + 1] > arr[l] ? l + 1 : l;
            // 上面已经评选了最强的孩子，接下来，当前的数和最强的孩子之前，最强下标是谁
            best = arr[best] > arr[i] ? best : i;
            // 如果最强的下标，是当前的数，那么当前的数已经满足大根堆结构，退出
            if (best == i) { // 最强的是自己
                break;
            }
            swap(arr, best, i);
            i = best;
            l = i * 2 + 1;
        }
    }
    void swap(vector<int>& arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
    // 从顶到底建立大根堆，O(n * logn)
    // 依次弹出堆内最大值并排好序，O(n * logn)
    // 整体时间复杂度O(n * logn)
    void heapSort1(vector<int>& arr) {
        int n = arr.size();
        for (int i = 0; i < n; i++) {
            heapInsert(arr, i);
        }
        int size = n;
        while (size > 1) {
            swap(arr, 0, --size);
            heapify(arr, 0, size);
        }
    }
};
int main() {
    //vector<int> arr = { 10,0,20,5,89,70,65,45 };
    //vector<int> arr = { 20,30,15,10,9,8,12,45,0,23 };
    vector<int> arr = { 5,6,3,1,9,2,4,6 };
    heapSort hs;
    vector<int> res = hs.sortArray(arr);
    for (int i = 0; i < res.size(); i++) {
        cout << res[i] << " ";
    }
    cout << endl;
    return 0;
}

三、从底到顶建立大根堆

依次弹出堆内最大值并排好序

完整代码：

#include <iostream>
using namespace std;
#include <vector>
// 堆结构和堆排序，填函数练习风格
![](https://wy-static.wenxiaobai.com/chat-rag-image/17851754762988714151)
// 测试链接 : https://leetcode.cn/problems/sort-an-array/
class heapSort {
public:
    vector<int> sortArray(vector<int> arr) {
        if (arr.size() > 1) {
            // heapSort1 为从顶到底建堆然后排序
            // heapSort2 为从底到顶建堆然后排序
            // 用哪个都可以
            //heapSort1(arr);
            heapSort2(arr);
        }
        return arr;
    }
    // i位置的数，向上调整大根堆
    // arr[i] = x，x是新来的！往上看，直到不比父亲大，或者来到0位置(顶)
    void heapInsert(vector<int>& arr, int i) {
        // i -> 父: (i - 1) / 2
        while (arr[i] > arr[(i - 1) / 2]) {
            swap(arr, i, (i - 1) / 2);
            i = (i - 1) / 2;
        }
    }
    // i位置的数，变小了，又想维持大根堆结构
    // 向下调整大根堆
    // 当前堆的大小为size
    void heapify(vector<int>& arr, int i, int size) {
        int l = i * 2 + 1;
        
        while (l < size) {
            // 有左孩子，l
            // 右孩子，l+1
            // 评选，最强的孩子，是哪个下标的孩子
            int best = l + 1 < size && arr[l + 1] > arr[l] ? l + 1 : l;
            // 上面已经评选了最强的孩子，接下来，当前的数和最强的孩子之前，最强下标是谁
            best = arr[best] > arr[i] ? best : i;
            // 如果最强的下标，是当前的数，那么当前的数已经满足大根堆结构，退出
            if (best == i) { // 最强的是自己
                break;
            }
            swap(arr, best, i);
            i = best;
            l = i * 2 + 1;
        }
    }
    void swap(vector<int>& arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
    // 从底到顶建立大根堆，O(n)
    // 依次弹出堆内最大值并排好序，O(n * logn)
    // 整体时间复杂度O(n * logn)
    void heapSort2(vector<int>& arr) {
        int n = arr.size();
        for (int i = n - 1; i >= 0; i--) {
            heapify(arr, i, n);
        }
        int size = n;
        while (size > 1) {
            swap(arr, 0, --size);
            heapify(arr, 0, size);
        }
    }
};
int main() {
    //vector<int> arr = { 10,0,20,5,89,70,65,45 };
    //vector<int> arr = { 20,30,15,10,9,8,12,45,0,23 };
    vector<int> arr = { 5,6,3,1,9,2,4,6 };
    heapSort hs;
    vector<int> res = hs.sortArray(arr);
    for (int i = 0; i < res.size(); i++) {
        cout << res[i] << " ";
    }
    cout << endl;
    return 0;
}

四、计算复杂度

总结堆结构

完全二叉树和数组前缀范围的对应
i的父亲节点：(i-1)/2，i的左孩子：i2+1，i的左孩子：i2+2
堆的定义（大根堆，小根堆），本节课讲解按照大根堆来讲解，小根堆是同理的
堆的调整：heapInsert（向上调整），heapify（向下调整）
heapInsert、heapify方法的单次调用，时间复杂度O(logn)，完全二叉树的结构决定的

堆排序

A.从顶到底建堆，时间复杂度O(nlogn)，log1 + log2 + log3 + ... + logn -> O(nlogn)
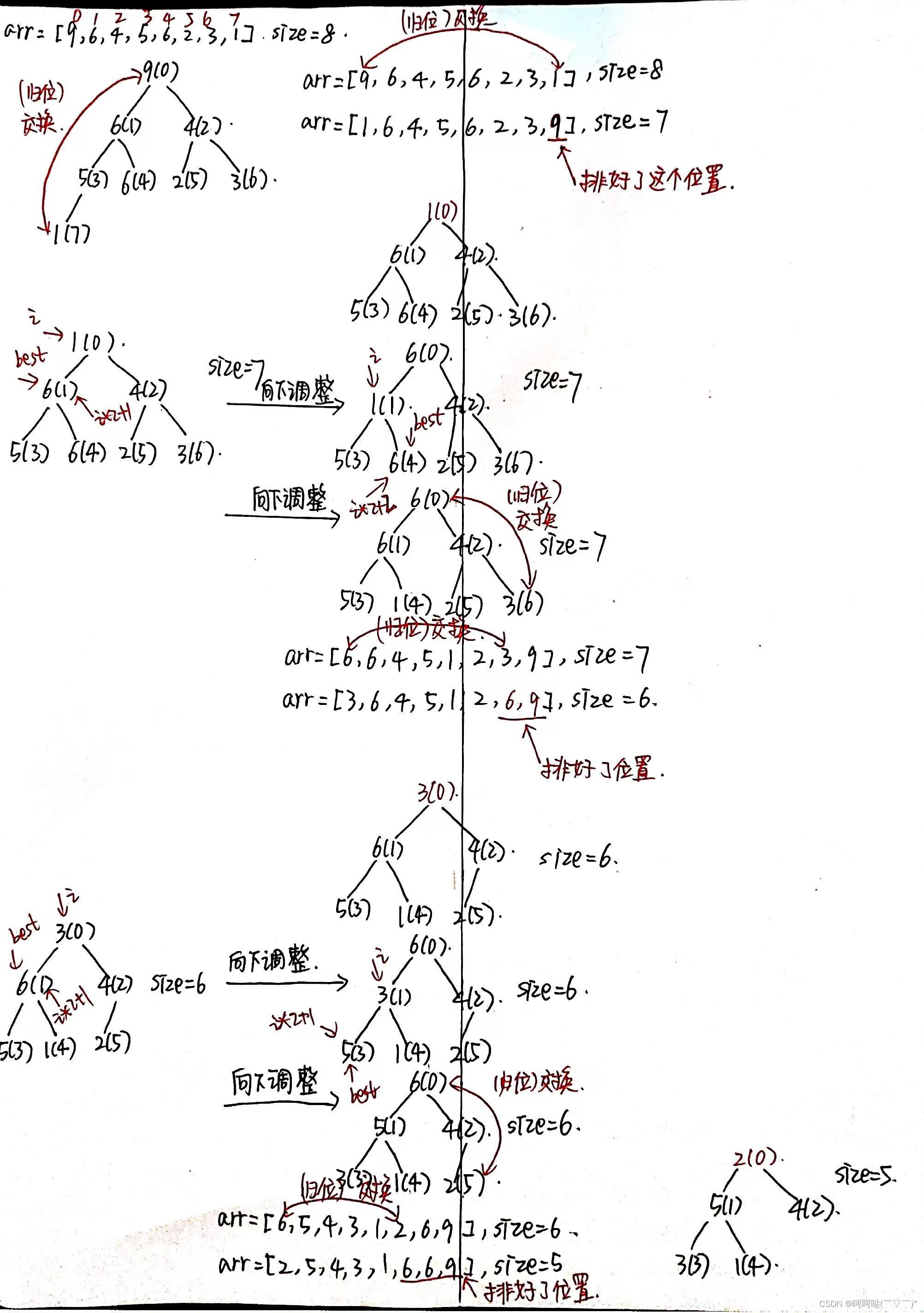
B.从底到顶建堆，时间复杂度O(n)，总代价就是简单的等比数列关系，为啥会有差异？简单图解一下
C.建好堆之后的调整阶段，从最大值到最小值依次归位，时间复杂度O(n*logn)，不管以什么方式建堆，调整阶段的时间复杂度都是这个，所以整体复杂度也是这个额外空间复杂度是O(1)，因为堆直接建立在了要排序的数组上，所以没有什么额外空间

注意:堆结构比堆排序有用的多，尤其是和比较器结合之后，后面博客会重点讲述